
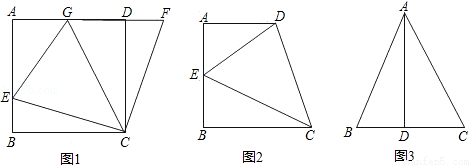
��ͼ1����������ABCD�У�E��AB��һ�㣬F��AD�ӳ�����һ�㣬��DF=BE��
��1����֤��CE=CF��
��2����ͼ1�У���G��AD�ϣ�����GCE=45�㣬��GE=BE+GD������Ϊʲô��
��3����������ѧ��֪ʶ�����ã�1������2������л��۵ľ��飬������и��⣺
����ͼ2����ֱ������ABCD�У�AD��BC��BC��AD������B=90�㣬AB=BC=12��E��AB���е㣬����DCE=45�㣬��DE�ij���
����ͼ3������ABC�У���BAC=45�㣬AD��BC��BD=2��CD=3������ABC�����Ϊ��_________����ֱ��д�����������Ҫд��������̣���
��1��֤����������
��2��GE=BE+GD���������ɼ�������
��3����DE=10��
����ABC�����Ϊ15��
��������
�����������1����ΪABCDΪ�����Σ�����CB=CD����B=��CDA=90�㣬����ΪDF=BE������BCE�ա�DCF��������֤CE=CF��
��2����Ϊ��BCD=90�㣬��GCE=45�㣬������BCE+��GCD=45�㣬����Ϊ��BCE�ա�DCF��������ECG=��FCG��CE=CF��CG=CG������ECG�ա�FCG����GE=BE+GD������
��3��������C��CG��AD��AD���ӳ����ڵ�G�����ù��ɶ������DE�ij���
������������������ͼ�Σ�������֪���������ù��ɶ��������AD�ij����������ABC�������
�����������1��֤������������ABCD�� CB=CD����B=��CDA=90�㣬
���CDF=��B=90�㣮
����BCE����DCF��
 ��
��
���BCE�ա�DCF��SAS����
��CE=CF��

��2��GE=BE+GD�������������£�
�ߡ�BCD=90�㣬��GCE=45�㣬
���BCE+��GCD=45�㣮
�ߡ�BCE�ա�DCF����֤����
���BCE=��DCF��
���GCF=��GCD+��DCF=��GCD+��BCE=45�㣮
���ECG=��FCG=45�㣮
����ECG����FCG��
 ��
��
���ECG�ա�FCG��SAS����
��GE=FG��
��FG=GD+DF��
��GE=BE+GD��
��3������ͼ2������C��CG��AD��AD���ӳ����ڵ�G��
�ɣ�2��������֪��DE=DG+BE��
��DG=x����AD=12��x��DE=x+6��
��Rt��ADE�У��ɹ��ɶ������ã�
AD2+AE2=DE2
��62+��12��x��2=��x+6��2
���x=4��
��DE=6+4=10��
������ABD����AB���۵���ʹD��E�غϣ���ACD����AC���۵���ʹD��G�غϣ�
�ɵ���BAD=��EAB����DAC=��GAC��
���EAG=��E=��G=90�㣬
AE=AG=AD��
BD=EB=2��
DC=CG=3��
���ı���AEFGΪ�����Σ�
�������εı߳�Ϊx��
�ɵ�BF=x��2��CF=x��3��
��Rt��BCF��
���ݹ��ɶ����ã�
BF2+CF2=BC2��
����x��2��2+��x��3��2=��2+3��2��
��ã�x=6��x=��1����ȥ����
��AD=6��
��S��ABC= BC•AD=15��
BC•AD=15��

���㣺1.���������ε��ж�2.ȫ�������ε��ж�������3.���ɶ���4.�����ε��ж���


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡʯ��ׯ�а��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
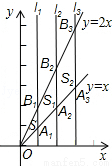
��ͼ��ֱ��l1��x���ڵ㣨1��0����ֱ��l2��x���ڵ㣨2��0����ֱ��l3��x���ڵ㣨3��0������ֱ��ln��x���ڵ㣨n��0��������y=x��ͼ����ֱ��l1��l2��l3��ln�ֱ��ڵ�A1��A2��A3����An������y=2x��ͼ����ֱ��l1��l2��l3��ln�ֱ��ڵ�B1��B2��B3��Bn�������OA1B1���������S1���ı���A1A2B2B1���������S2���ı���A2A3B3B2���������S3���ı���An��1AnBnBn��1���������Sn����ôS2014=��_________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ�����ذ��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪����ƽ���ڵ�M( a, b )�ڵ������ޣ���ô��N( b, ��a )�ڣ� ��
A���������� B���������� C���ڶ����� D����һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ��ɽ�а��꼶��ѧ����ĩ����ѧ�Ծ��������棩 ���ͣ�ѡ����
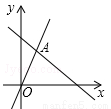
��ͼ������y=2x��y=ax��4��ͼ���ཻ�ڵ�A��m��3������ʽ2x��ax��4�Ľ⼯Ϊ �� ��
A��x��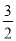 B��x��3 C��x����
B��x��3 C��x����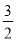 D��x��3
D��x��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ��ɽ�а��꼶��ѧ����ĩ����ѧ�Ծ��������棩 ���ͣ�ѡ����
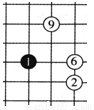
��ͼ1��һ��Χ������ļ�����.Ϊ��¼�����㣬���������ֱ�ʾ����������ĸ��ʾ������������ ��λ�ÿɼ�Ϊ��B,2��������ڵ�λ�ÿɼ�Ϊ(D,1)���������λ��Ӧ��Ϊ�� ��
��λ�ÿɼ�Ϊ��B,2��������ڵ�λ�ÿɼ�Ϊ(D,1)���������λ��Ӧ��Ϊ�� ��
A����C��5�� B��(C��4) C��(4��C) D��(5��C)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�߰��а��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��֪һ�κ���y=kx+b����x=2ʱ��y=��3����x=1ʱ��y=��1��
��1����һ�κ����Ľ���ʽ��
��2������һ�κ�����ͼ�ν�x��y��ֱ���A��B���㣬����ABO�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�߰��а��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��һ�����ݣ�7��9��6��x��8��7��5�ļ�����6����ôx��ֵ�ǡ�_________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ���꼶��ѧ����ѧ������ѧ�Ծ��������棩 ���ͣ������
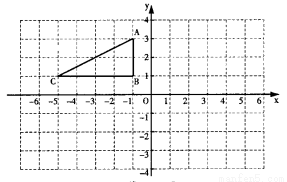
��ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��
��1������ABC����ƽ��6����λ�õ���A1B1C1���뻭����A1B1C1����д����C1�����ꣻ
��2������ABC��ԭ��O��ת180��õ���A2B2C2���뻭����A2B2C2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ���꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
���������ε�һ��Ϊ4����һ��Ϊ9������������ε��ܳ�Ϊ �� ��
A��17 B��22 C��13 D��17��22
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com