

���� ��֪���ɡ�ABC�ǵȱ������Σ��ɵ�AC=CB����ACE=��B=60�㣬����BD=CE������֤�á�ACE�ա�CBD��
̽�������ݡ�ABC�ǵȱ������Σ��õ�AC=CB����A=��ACB=60�㣬��SAS֤����ACE�ա�CBD��
Ӧ�ã�֤����ACE�ա�CBD���õ���AEC=��CDB=�£�������ǵ����ʵõ���CAB=��ACE+��AEC�����ɽ��
��� �⣺��֪���ߡ�ABC�ǵȱ������Σ�
��AC=CB����CAE=��B=60�㣬
�ڡ�ACE�͡�CBD�У�
$\left\{\begin{array}{l}{AC=CB}\\{��CAE=��B}\\{CE=BD}\end{array}\right.$
���ACE�ա�CBD��SAS����
̽������ACE���CBD�Ƿ���Ȼȫ�ȣ�
�ߡ�ABC�ǵȱ������Σ�
��AC=CB����A=��ACB=60�㣬
���EAC=��DCB��
�ڡ�ACE�͡�CBD�У�
$\left\{\begin{array}{l}{AE=CD}\\{��EAC=��DCB}\\{AC=BC}\end{array}\right.$
���ACE�ա�CBD��
Ӧ�ã��ߵ�O��AC�ߵĴ�ֱƽ������BC�Ľ��㣬
��CO=AO��
���ACB=��CAO=����
�ߡ�ACB+��BCD=180�㣬��EAC+��CAO=180�㣬
���EAC=��DCB��
�ߡ�ABCΪ�ȱ������Σ�
��AC=BC��
�ڡ�EAC�͡�DCB�У�
$\left\{\begin{array}{l}{AE=CD}\\{��EAC=��BCD}\\{AC=CB}\end{array}\right.$
���EAC�ա�DCB��
���AEC=��CDB=�£�
�ߡ�CAB=��ACE+��AEC��
���ACE=��CAB-��AEC=��-�£�
�ʴ�Ϊ����-�£�
���� ���⿼����ȫ�������ε����ʶ������ж��������������Ĺؼ���֤����EAC�ա�DCB��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
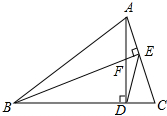 ��ͼ��AD��BC������ΪD��BE��AC������ΪE��AD��BE�ཻ�ڵ�F������DE��
��ͼ��AD��BC������ΪD��BE��AC������ΪE��AD��BE�ཻ�ڵ�F������DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0=1 | B�� | $\sqrt{x^2}=x$ | C�� | 2-2=-4 | D�� | -|-2|=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ֱ��l1��l2����A=50�㣬��1=45�㣬���2�Ķ���Ϊ��������
��ͼ��ֱ��l1��l2����A=50�㣬��1=45�㣬���2�Ķ���Ϊ��������| A�� | 95�� | B�� | 85�� | C�� | 65�� | D�� | 45�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-5��-2�� | B�� | ��5��2�� | C�� | ��-5��2�� | D�� | ��2��5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com