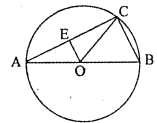
[题目]如图.AB是⊙O的直径.弦BC=9.∠BOC=50°.OE⊥AC.垂足为E． (1)求OE的长．(2)求劣弧AC的长．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，AB是⊙O的直径，弦BC=9，∠BOC=50°，OE⊥AC，垂足为E．

（1）求OE的长．

（2）求劣弧AC的长(结果精确到0．1)．

【答案】（1）4.5（2）24.2

【解析】（1）∵OE⊥AC，OE为直径的一部分

∴AE=EC （2分）

又∵AO=BO

∴（2分）

（2）∵∠COB=50°

∴∠AOC=130° （1分）

∵AO=CO，OE⊥AC

∴∠AOE=∠AOC =65°（2分）

∴

∴AO=（1分）

∴（2分）

（1）由垂径定理知，由E是AC的中点，点O是AB的中点，则OB是△ABC的BC边对的中位线，所以OE=BC÷2；

（2）由圆周角定理得，∠A=∠BDC=25°，由等边对等角得∠OCA=∠A，由三角形内角和定理求得∠AOC的度数，再利用弧长公式求得弧AC的长．

练习册系列答案

宇轩图书小学毕业升学系统总复习系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】某校七年级班有人，班比班人数的2倍少8人，如果从班调出6人到班.

（1）用代数式表示两个班共有多少人？

（2）用代数式表示调动后，班人数比班人数多几人？

（3）等于多少时，调动后两班人数一样多？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．

（1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE= 度；

（2）设∠BAC= ，∠DCE= ．

① 如图2，当点D在线段CB上，∠BAC≠90°时，请你探究与之间的数量关系，并证明你的结论；

② 如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时与之间的数量关系（不需证明）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知∠ABC=90°，D是直线AB边上的点，AD=BC

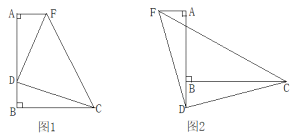
（1）如图1，点D在线段AB上，过点A作AF⊥AB，且AF=BD，连接DC、DF、CF，试判断△CDF的形状并说明理由；

（2）如图2，点D在线段AB的延长线上，点F在点A的左侧，其他条件不变，以上结论是否仍然成立？请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为进一步推动我县校园足球运动的发展，提高全县中小学生足球竞技体育水平，选拔和培养优秀足球后备人才，增强青少年体质，进一步营造全社会关注青少年足球运动的氛围，汶上县第五届“县长杯”校园足球比赛于2019年11月9日—11月24日成功举办．我县县城区四校决定联合购买一批足球运动装备，市场调查发现，甲、乙两商场以同样的价格出售同种品牌的足球队服和足球，已知每套队服比每个足球多50元，两套队服与三个足球的费用相等，经洽谈，甲商场优惠方案是：每购买十套队服,送一个足球，乙商场优惠方案是：若购买队服超过80套，则购买足球打八折．

（1）求每套队服和每个足球的价格分别是多少；

（2）若城区四校联合购买100套队服和个足球，请用含的式子分别表示出到甲商场和乙商场购买装备所花的费用；