
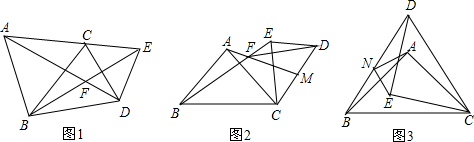
| BC |
| AC |
| CE |
| CM |
| BE |
| AM |
| BC |
| AC |
| 2 |
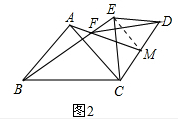
| 2 |
| 2 |
| BC |
| AC |
| 2 |
| CE |
| CM |
| BE |
| AM |
| BC |
| AC |
| 2 |
| 2 |
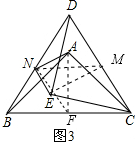
| 1 |
| 2 |
| 1 |
| 2 |
|


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 届数 | 金牌 | 银牌 | 铜牌 | 总计 |
| 第23届 | 15 | 8 | 9 | 32 |
| 第24届 | 5 | 11 | 12 | 28 |
| 第25届 | 16 | 22 | 16 | 54 |
| 第26届 | 16 | 22 | 12 | 50 |
| 第27届 | 28 | 16 | 15 | 59 |
| 第28届 | 32 | 17 | 14 | 63 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,∠AMB=90°,∠CMD=90°,ME、MF分别是射线MA、MD的反向延长线.
如图,∠AMB=90°,∠CMD=90°,ME、MF分别是射线MA、MD的反向延长线.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
已知△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
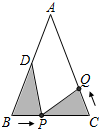 如图,在△ABC中,AB=AC=12,BC=8,D为AB的中点,点P在线段BC上以每秒2个单位的速度由B点向C点运动,同时,点Q在线段CA上以每秒x个单位的速度由C点向A点运动.当△BPD与以C、Q、P为顶点的三角形全等时,x的值为
如图,在△ABC中,AB=AC=12,BC=8,D为AB的中点,点P在线段BC上以每秒2个单位的速度由B点向C点运动,同时,点Q在线段CA上以每秒x个单位的速度由C点向A点运动.当△BPD与以C、Q、P为顶点的三角形全等时,x的值为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com