
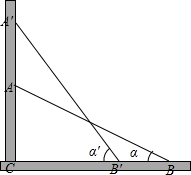
 如图,一根3m长的竹竿AB斜靠在墙上,当端点A离地面的高度AC长为1m时,竹竿AB的倾斜角α的正切tanα的值是多少?当端点A位于A′,离地面的高度A′C为2m时,倾斜角α′的正切tanα′的值是多少?tanα的值可以大于100吗?
如图,一根3m长的竹竿AB斜靠在墙上,当端点A离地面的高度AC长为1m时,竹竿AB的倾斜角α的正切tanα的值是多少?当端点A位于A′,离地面的高度A′C为2m时,倾斜角α′的正切tanα′的值是多少?tanα的值可以大于100吗? 分析 根据题意可以求得AC、BC的长度,从而可以求得BC的长,从而可得tanα的值,同理可得tanα′的值,根据一个锐角的正切值随着这个角的增大而增大,从而可知tanα的值是否可以大于100.
解答 解:由题意可得,∠ACB=90°,AB=3,AC=1,
∴$BC=\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}=2\sqrt{2}$.
∴tanα=$\frac{AC}{BC}=\frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{4}$.
∵∠A′CB′=90°,A′B′=AB=3,A′C=2,
∴$B′C=\sqrt{A′B{′}^{2}-A′{C}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$.
∴tanα′=$\frac{A′C}{B′C}=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$.
∵tanα=$\frac{AC}{BC}$,当AC很大时,则BC就很小,
∴tanα的值可以大于100.
点评 本题考查解直角三角形的应用,解题的关键是将题目中的条件进行转化,得到所求问题需要的条件,知道一个锐角的正切值随着这个角的增大而增大.


科目:初中数学 来源: 题型:解答题
 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点B、C的坐标分别为(-2,0),(-1,2).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点B、C的坐标分别为(-2,0),(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (y-x)(x-y) | B. | (x-y)(x-y+1) | C. | (x-y)(x-y-1) | D. | (x-y)(y-x-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a+2b | B. | 2b-2a | C. | 2b | D. | 4b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<$\frac{1}{3}$ | B. | x>$\frac{1}{3}$ | C. | x<0 | D. | x>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
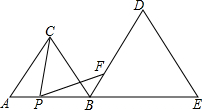 等边△ABC和等边△BDE,A、B、E在同-直线上,P是直线AB上一动点,从A向B方向移动.∠CPF=∠A,PF交射线BD于F.
等边△ABC和等边△BDE,A、B、E在同-直线上,P是直线AB上一动点,从A向B方向移动.∠CPF=∠A,PF交射线BD于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com