
【题目】“全民防控新冠病毒”期间某公司推出一款消毒产品,成本价8元/千克,经过市场调查,该产品的日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
(元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
销售单价 | 12 | 16 | 20 | 24 |
日销售量 | 220 | 180 | 140 |
|
(注:日销售利润![]() 日销售量
日销售量![]() (销售单价
(销售单价![]() 成本单价)
成本单价)
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出
的函数解析式(不要求写出![]() 的取值范围);
的取值范围);
(2)根据以上信息,填空:
①![]() _______千克;
_______千克;
②当销售价格![]() _______元时,日销售利润
_______元时,日销售利润![]() 最大,最大值是_______元;
最大,最大值是_______元;
(3)该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象,为了保证捐赠后每天的剩余利润不低于1500元,试确定该产品销售单价的范围.
【答案】(1)![]() ;(2)①100;②21,1690;(3)该产品销售单价的范围为
;(2)①100;②21,1690;(3)该产品销售单价的范围为![]() .
.
【解析】
(1)设y关于x的函数解析式为y=kx+b,由待定系数法求解即可;
(2)①将x=24代入一次函数解析式,计算即可得出m的值;②根据日销售利润=日销售量×(销售单价-成本单价)写出函数关系式,并将其配方,写成顶点式,按照二次函数的性质可得答案;
(3)根据题意,W=-10x2+420x-2720-100≥1500,变形得出关于x的不等式,再根据二次函数的性质可得答案.
解:(1)设y关于x的函数解析式为y=kx+b,将(12,220),(16,180)代入得:
![]() ,解得
,解得![]() .
.
∴y=-10x+340;
(2)①∵当x=24时,y=-10×24+340=100,
∴m=100.
故答案为:100;
②由题意得:
W=(-10x+340)(x-8)=-10x2+420x-2720=-10(x-21)2+1690,
∵-10<0,
∴当x=21时,W有最大值为1690元.
故答案为:21,1690;
(3)由题意得:
W=-10x2+420x-2720-100≥1500,
∴x2-42x+432≤0,
当x2-42x+432=0时,
解得:x1=18,x2=24,
∵函数y=x2-42x+432的二次项系数为正,图象开口向上,
∴18≤x≤24,
∴该产品销售单价的范围为18≤x≤24.


科目:初中数学 来源: 题型:
【题目】小魏探究学习函数的经验,对函数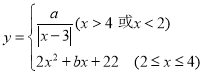 的图像与性质进行了研究,下面是小魏的探究过程,请补充完整.
的图像与性质进行了研究,下面是小魏的探究过程,请补充完整.
(1)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请直接写出:![]() _______,
_______,![]() ______,
______,![]() _______.
_______.
(2)画出该函数图像.
(3)写出该函数的一条性质:_______________.
(4)一次函数![]() 与该函数图像至少有三个交点,则
与该函数图像至少有三个交点,则![]() 的范围_______.
的范围_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.
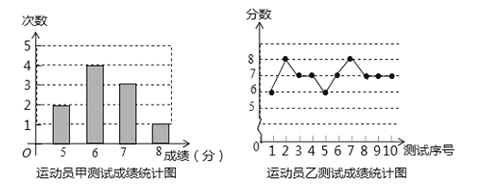
运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
运动员丙测试成绩的平均数和众数都是7,
(1)成绩表中的![]() __________,
__________,![]() _________;
_________;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球从乙手中传出,球传一次甲得到球的概率是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节假日期间向、某商场组织游戏,主持人请三位家长分别带自己的孩于参加游戏,A、B、C分别表示一位家长,他们的孩子分别对应的是a,b,![]() 若主持人分别从三位家长和三位孩予中各选一人参加游戏.
若主持人分别从三位家长和三位孩予中各选一人参加游戏.
![]() 若已选中家长A,则恰好选中自己孩子的概率是______.
若已选中家长A,则恰好选中自己孩子的概率是______.
![]() 请用画树状图或列表法求出被选中的恰好是同一家庭成员的概率.
请用画树状图或列表法求出被选中的恰好是同一家庭成员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州中学在“读书日”期间购进一批图书, 需要用大小两种规格的纸箱来装运.![]() 个大纸箱和
个大纸箱和![]() 个小纸箱一次可以装
个小纸箱一次可以装![]() ,本书
,本书![]() 个大纸箱和
个大纸箱和![]() 个小纸箱--次可以装
个小纸箱--次可以装![]() 本书.
本书.
(1)一个大纸箱和一个小纸箱分别可以装多少本书?
(2)如果一共购入![]() 本书,每个纸箱恰好装满,分别需要用多少个大、小纸箱?
本书,每个纸箱恰好装满,分别需要用多少个大、小纸箱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销量较好的肉馅粽(咸)、豆沙馅粽(甜)、红枣馅粽(甜)、蛋黄馅粽(咸)(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
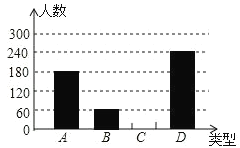
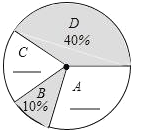
请根据以上信息回答:
(1)本次参加抽样调查的市民有多少人?
(2)将两幅不完整的图补充完整;
(3)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他吃到的两个粽子都是甜味的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线y=ax2+bx+3与x轴交于点A(3,0),B(﹣1,0),与y轴交于点C,连接AC,点P是直线AC上方的抛物线上一动点(异于点A,C),过点P作PE⊥x轴,垂足为E,PE与AC相交于点D,连接AP.
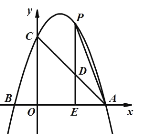
(1)求点C的坐标;
(2)求抛物线的解析式;
(3)①求直线AC的解析式;
②是否存在点P,使得△PAD的面积等于△DAE的面积,若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C′处,若∠ADB=46°,则∠DBE的度数为 °.
(2)小明手中有一张矩形纸片ABCD,AB=4,AD=9.
(画一画)
如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
(算一算)
如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A′,B′处,若AG=![]() ,求B′D的长;
,求B′D的长;
(验一验)
如图4,点K在这张矩形纸片的边AD上,DK=3,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点A′,B′处,小明认为B′I所在直线恰好经过点D,他的判断是否正确,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com