练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某游乐场试营业期间，每天运营成本为1000元.经统计发现，每天售出的门票张数（张）与门票售价（元/张）之间满足一次函数，设游乐场每天的利润为（元）.（利润=票房收入－运营成本）

    （1）试求与之间的函数表达式.

    （2）游乐场将门票售价定为多少元/张时，每天获利最大？最大利润是多少元？

    【答案】（1）w=;（2）游乐场将门票售价定为25元/张时，每天获利最大，最大利润是1500元

    【解析】

    （1）根据及利润=票房收入－运营成本即可得出化简即可.

    （2）根据二次函数的性质及对称轴公式即可得最大值，及x的值.

    （1）根据题意，得.

    （2）∵中，，

    ∴有最大值.

    当时，最大，最大值为1500.

    答：游乐场将门票售价定为25元/张时，每天获利最大，最大利润是1500元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+3在坐标系中的位置如图所示，它与x，y轴的交点分别为A，B，P是其对称轴x=1上的动点，根据图中提供的信息，给出以下结论：①2a+b=0，②x=3是ax2+bx+3=0的一个根，③△PAB周长的最小值是+3．其中正确的是（　　）

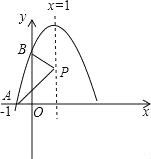
    A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

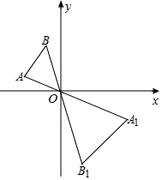
    【题目】如图，已知△AOB和△A1OB1是以点O为位似中心的位似图形，且△AOB和△A1OB1的周长之比为1：2，点B的坐标为（-1，2），则点B1的坐标为（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①是一种包装盒的表面展开图，将它围起来可得到一个几何体的模型．

    (1)请说出这个几何体模型的最确切的名称是__ __；

    (2)如图②是根据 a，h的取值画出的几何体的主视图和俯视图(图中的粗实线表示的正方形(中间一条虚线)和三角形)，请在网格中画出该几何体的左视图；

    (3)在(2)的条件下，已知h＝20 cm，求该几何体的表面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在路灯下，小明的身高如图中线段AB所示，他在地面上的影子如图中线段AC所示，小亮的身高如图中线段FG所示，路灯灯泡在线段DE上．

    （1）请你确定灯泡所在的位置，并画出小亮在灯光下形成的影子．

    （2）如果小明的身高AB=1.6m，他的影子长AC=1.4m，且他到路灯的距离AD=2.1m，求灯泡的高.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某小区开展了“行车安全，方便居民”的活动，对地下车库作了改进．如图，这小区原地下车库的入口处有斜坡AC长为13米，它的坡度为i＝1：2.4，AB⊥BC，为了居民行车安全，现将斜坡的坡角改为13°，即∠ADC＝13°（此时点B、C、D在同一直线上）．

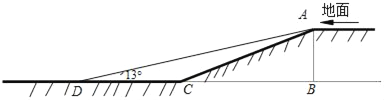
    （1）求这个车库的高度AB；

    （2）求斜坡改进后的起点D与原起点C的距离（结果精确到0.1米）．

    （参考数据：sin13°≈0.225，cos13°≈0.974，tan13°≈0.231，cot13°≈4.331）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，点A（3，3），点B（4，0），点C（0，﹣1）．

    （1）以点C为中心，把△ABC逆时针旋转90°，请在图中画出旋转后的图形△A′B′C，点B′的坐标为________；

    （2）在（1）的条件下，求出点A经过的路径的长（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

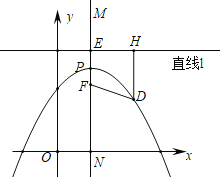
    【题目】寻找神奇点！每条抛物线内都有一个神奇的点F（也叫焦点），还有一条与之配套的直线！（也叫准线），使得抛物线上的每个点到F的距离等于到直线l的距离．如图，对于抛物线上任意一点D，都有DF＝DH．

    根据以上知识，我们来完成以下问题：

    （1）因为抛物线是轴对称图形，由对称性可知这个神奇的点F应在抛物线的　 　上，且准线l一定与对称轴垂直即l⊥MN（对称轴）．

    （2）若准线l与对称轴MN交于E，MN交抛物线于点P，则PE、PF的数量关系是PE　 　PF（填＞、＝、＜），

    （3）求抛物线y＝﹣（x﹣2）2+4的神奇点（焦点）F的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

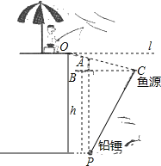
    【题目】如图所示，老张利用国庆假日在某钓鱼场钓鱼，风平浪静时，鱼漂露出水面部分AB＝6m，微风吹来时，假设铅锤P不动，鱼漂移动了一段距离BC，且项場恰好与水面平齐（即PAPC，水平线1与OC夹角a＝8°（点A在OC上，则铅锤P处的水深h为（　　）（参考数据：sin8°＝，cos8°＝，tan8°＝）

    A.150cmB.144cmC.111cmD.105cm

    查看答案和解析>>

    同步练习册答案