
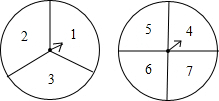
 两个自由转动的转盘如图所示,一个分为3等份,分别标有数字1,2,3,另一个分为4等份,分别标有数字4,5,6,7.转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面A,B两种方案中选一种:方案A:猜“奇数”或猜“偶数”其中的一种;方案B:猜“是3的整数倍”或猜“不是3的整数倍”其中的一种.
两个自由转动的转盘如图所示,一个分为3等份,分别标有数字1,2,3,另一个分为4等份,分别标有数字4,5,6,7.转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面A,B两种方案中选一种:方案A:猜“奇数”或猜“偶数”其中的一种;方案B:猜“是3的整数倍”或猜“不是3的整数倍”其中的一种.分析 (1)列举出所有情况,分别得到相应的概率,比较即可;
(2)应选择获胜概率相同的游戏进而得出答案.
解答 解:(1)选择B的猜数的方案,并且猜“和不是3的整数倍”.
列树状图如下: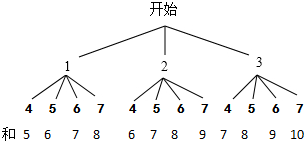
共有12种可能结果,且每种结果出现的可能性相同.
方案A:由树状图可得,和为奇数以及和为偶数的结果分别是6种,
所以P(和为奇数)=$\frac{6}{12}=\frac{1}{2}$; P(和为偶数)=$\frac{6}{12}=\frac{1}{2}$;
方案B:由树状图可得,和是3的整数倍有4种,即为6,6,9,9
所以P(和是3的整数倍)=$\frac{4}{12}=\frac{1}{3}$;P(和不是3的整数倍)=$\frac{8}{12}=\frac{2}{3}$.
所以,我选择B的猜数的方案,并且猜“和不是3的整数倍”,因为此时获胜的概率为$\frac{2}{3}$,获胜的可能性最大.
(2)为了保证游戏的公平性,应该选择方案A.
因为P(和为奇数)=P(和为偶数)=$\frac{1}{2}$,
所以,选择方案A的猜数方法对双方是公平的.
点评 此题主要考查了游戏公平性,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$,注意本题是放回实验.解决本题的关键是得到相应的概率,概率相等就公平,否则就不公平.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
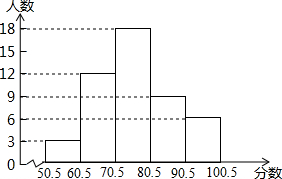 某校一次知识竞赛,竞赛成绩(取整数),进行整理后分五组,并绘制成频数分布直方图,结合图形,解答下列问题:
某校一次知识竞赛,竞赛成绩(取整数),进行整理后分五组,并绘制成频数分布直方图,结合图形,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
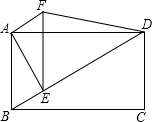 如图,四边形ABCD是矩形,E是对角线BD上不同于B,D的任意一点,AF=BE,∠DAF=∠CBD.
如图,四边形ABCD是矩形,E是对角线BD上不同于B,D的任意一点,AF=BE,∠DAF=∠CBD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
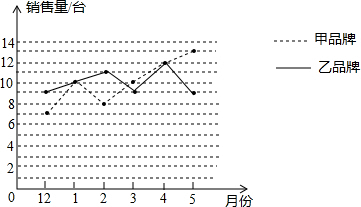
| 平均数 | 方差 | |
| 甲品牌销售量/台 | 10 | $\frac{13}{3}$ |
| 乙品牌销售量/台 | 10 | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com