
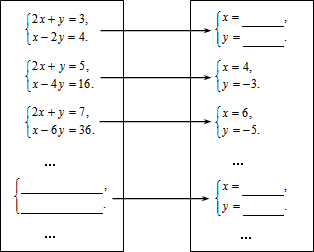
���� ��1��������Ԫ�����Ԫһ�η����鼴�ɣ�
��2�����ݷ�������xyϵ���ı仯���ɿɵó���n�������飻
��3�����ݸ�������Ľ�ı仯���ɵó�������Ľ⼴�ɣ�
��� �⣺��1��$\left\{\begin{array}{l}2x+y=3��\\ x-2y=4��\end{array}\right.$��
�ɢڵ�x=2y+4�ۣ�
�Ѣ۴���٣���2��2y+4��+y=3��
���y=-1��
��y=-1����۵�x=2��
���Է�����1�Ľ�Ϊ$\left\{\begin{array}{l}x=2\\ y=-1\end{array}\right.$��
�ʴ�Ϊ��2��-1��
��2��������n��$\left\{\begin{array}{l}2x+y=2n+1\\ x-2ny=4{n}^{2}\end{array}\right.$��
�ʴ�Ϊ��$\left\{\begin{array}{l}2x+y=2n+1\\ x-2ny=4{n}^{2}\end{array}\right.$��
��3�����Ľ�Ϊ$\left\{\begin{array}{l}x=2n\\ y=-2n+1\end{array}\right.$��
�ʴ�Ϊ��$\left\{\begin{array}{l}x=2n\\ y=-2n+1\end{array}\right.$��
���� ������Ҫ�����˶�Ԫһ�η�����Ľ��Լ�������֪������ó��������Ĺ��ɣ���ȷ���ֹ����ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
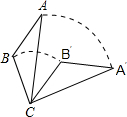 ��ͼ������ABC�Ƶ�C��ת60��õ���A��B��C����֪AC=6��BC=2$\sqrt{5}$�����߶�ABɨ����ͼ�ε����Ϊ��������
��ͼ������ABC�Ƶ�C��ת60��õ���A��B��C����֪AC=6��BC=2$\sqrt{5}$�����߶�ABɨ����ͼ�ε����Ϊ��������| A�� | �� | B�� | 3�� | C�� | 6�� | D�� | $\frac{8}{3}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3•a2=a5 | B�� | a6��a3=a2 | C�� | 3a+5b=8ab | D�� | 4a2-2a2=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
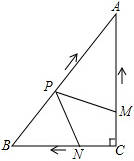 ��ͼ����Rt��ABC�У���C=90�㣬AC=4cm��BC=3cm������M��N�ӵ�Cͬʱ�������ֱ���CA��CB���յ�A��B�ƶ�����M���ٶ���ÿ��1cm��ͬʱ����P�ӵ�B��������ÿ��2cm���ٶ���BA���յ�A�ƶ������ƶ�ʱ��Ϊt��0��t��2.5���룬��tΪ��ֵʱ����A��P��MΪ����������ο������BPN���ƣ���ʱ��N���ٶ�ʱ���٣�
��ͼ����Rt��ABC�У���C=90�㣬AC=4cm��BC=3cm������M��N�ӵ�Cͬʱ�������ֱ���CA��CB���յ�A��B�ƶ�����M���ٶ���ÿ��1cm��ͬʱ����P�ӵ�B��������ÿ��2cm���ٶ���BA���յ�A�ƶ������ƶ�ʱ��Ϊt��0��t��2.5���룬��tΪ��ֵʱ����A��P��MΪ����������ο������BPN���ƣ���ʱ��N���ٶ�ʱ���٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
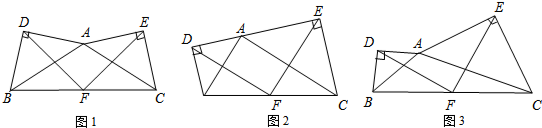
 ��֪����ͼ���ڡ�ABC�У�AB=AC����ABC����ACB��ƽ�����ཻ�ڵ�O������A0�����ӳ���BC���ڵ�D����֤��AD��BC��
��֪����ͼ���ڡ�ABC�У�AB=AC����ABC����ACB��ƽ�����ཻ�ڵ�O������A0�����ӳ���BC���ڵ�D����֤��AD��BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{4}$��3 | B�� | -1��6 | C�� | $-\frac{1}{4}$��5 | D�� | $\frac{1}{4}$��5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com