
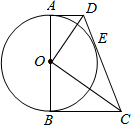
 如图,在梯形ABCD中,AD∥BC,∠B=90°,以AB为直径作⊙O,恰与一边CD相切于点E,连接OD、OC.若四边形ABCD的面积是48,设OD=x,OC=y,且x+y=14;
如图,在梯形ABCD中,AD∥BC,∠B=90°,以AB为直径作⊙O,恰与一边CD相切于点E,连接OD、OC.若四边形ABCD的面积是48,设OD=x,OC=y,且x+y=14;分析 (1)由切线的性质可知OE⊥DC,由HL可判定△OEC≌△OBC,从而可得到∠BCO=∠ECO,同理可证明∠ADO=∠EDO,从而可证明∠ODC+∠OCD=90°,由三角形的内角和定理可知∠DOC=90°;
(2)S梯形ABCD=2S△COD,求出xy=48,结合x+y=14可求得x2+y2=100,从而得到CD=10.
解答 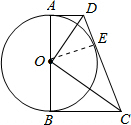 解:(1)如图所示:连接OE.
解:(1)如图所示:连接OE.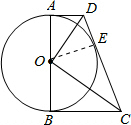
∵DC是圆O的切线,
∴OE⊥DC.
在Rt△OEC和Rt△OBC中,
$\left\{\begin{array}{l}{OE=OB}\\{OC=OC}\end{array}\right.$,
∴Rt△OEC≌Rt△OBC.
∴∠BCO=∠ECO.
∴∠OCD=$\frac{1}{2}∠BCD$.
同理:∠EDO=$\frac{1}{2}∠ADC$.
∵AD∥BC,
∴∠ADC+∠DCB=180°.
∴∠OCD+∠EDO=$\frac{1}{2}$×180°=90°.
∴∠DOC=90°.
(2)∵S△DEO=S△DAO,S△OCE=S△COB,
∴S梯形ABCD=2(S△DOE+S△COE)=2S△COD=OC•OD=48,即xy=48.
又∵x+y=1
∴x2+y2=(x+y)2-2xy=142-2×48=100,
在Rt△COD中,CD=$\sqrt{O{C}^{2}+O{D}^{2}}$=10,
∴CD=10.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理、圆周角定理和全等三角形的判定与性质,根据题意求得x2+y2=100是解题的关键.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
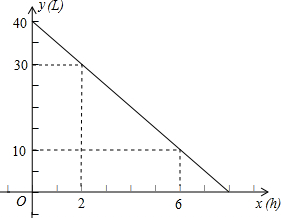 某种以汽油为燃料的机器,加满油并开始工作后,油箱中的余油量y(升)与工作时间x(小时)之间的函数关系如图所示.
某种以汽油为燃料的机器,加满油并开始工作后,油箱中的余油量y(升)与工作时间x(小时)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
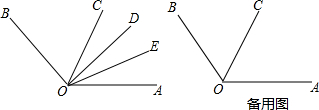 已知:OC平分∠AOB,以O为端点作射线OD,OE平分∠AOD,
已知:OC平分∠AOB,以O为端点作射线OD,OE平分∠AOD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
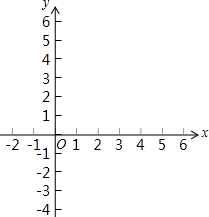 在平面直角系中,已知A(-2,0),B(0,4),C(3,6);
在平面直角系中,已知A(-2,0),B(0,4),C(3,6);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com