
����Ŀ����1����ֱ������ƽ���ڣ���֪��O�İ뾶ΪR����AΪ��O������һ�㣬����B��Բ��O�ľ���Ϊm���߶�AB�ij���Ϊl����m��Rʱ��l�����ֵ����Сֵ����Ϊ�� ������ ������m��Rʱ��l�����ֵ����Сֵ����Ϊ�� ������ ����
��2����ͼ����O�İ뾶Ϊ2����P�ġ�Kֵ���������£�����QΪ��O������һ�㣬�߶�PQ���ȵ����ֵ����Сֵ֮�Ϊ��P�ġ�Kֵ������ΪKP���ر�أ�����P��Q�غ�ʱ���߶�PQ�ij���Ϊ0��
������A��6��8����B����1��0������KA���� ����KB���� ����
����ֱ��y��2x��1�ϴ��ڵ�P��ʹ![]() �������P�ĺ����ꣻ
�������P�ĺ����ꣻ
��ֱ��![]() ��b��0����x�ᣬy��ֱ���A��B�����߶�AB�ϴ��ڵ�P��ʹ��
��b��0����x�ᣬy��ֱ���A��B�����߶�AB�ϴ��ڵ�P��ʹ��![]() ������ֱ��д��b��ȡֵ��Χ��
������ֱ��д��b��ȡֵ��Χ��
���𰸡���1��m+R��m��R��R+m��R��m����2����4��2����1��![]() ����1��b��2��
����1��b��2��
��������
��1����A��B��O��һ��ֱ����ʱ��AB��������Сֵ���ݴ˷ֱ���⼴�ɣ�
��2�����ȷֱ����AO��10��BO��1����KA����10+2������10��2����4��KB����2+1������2��1����2���ڵ���P��ԲO��ʱ��KP��2R��4�����������⣻����P��ԲO��ʱ��KP��2OP��2![]() ����P��m��2m��1��������m2+��2m��1��2��2��������m���۵�P����OΪԲ�ģ��뾶�ֱ�Ϊ
����P��m��2m��1��������m2+��2m��1��2��2��������m���۵�P����OΪԲ�ģ��뾶�ֱ�Ϊ![]() ��
��![]() Χ�ɵ�Բ���ڣ����߽磩�����߶�AB��ͼ����Ӱ�����й����㣬��
Χ�ɵ�Բ���ڣ����߽磩�����߶�AB��ͼ����Ӱ�����й����㣬��![]() ��b��0������OΪԲ�ģ�
��b��0������OΪԲ�ģ�![]() Ϊ�뾶��Բ����ʱ��
Ϊ�뾶��Բ����ʱ��![]() ��
��![]() �����b��1����
�����b��1����![]() ��b��0������OΪԲ�ģ�
��b��0������OΪԲ�ģ�![]() Ϊ�뾶��Բ����ʱ��
Ϊ�뾶��Բ����ʱ��![]() ��
��![]() �����b��2���Ӷ��ɵó�b��ȡֵ��Χ��
�����b��2���Ӷ��ɵó�b��ȡֵ��Χ��
�⣺��1����m��Rʱ����B��Բ�⣬
��ͼ2����A��B��O���㹲��ʱ��ABȡ�������Сֵ��
��A��Bλ��Բ��O����ʱABȡ�����ֵ�����ֵAB=BO+AO =m+R��
��A��Bλ��Բ��Oͬ��ʱABȡ����Сֵ����СֵAB=BO-AO=m��R��
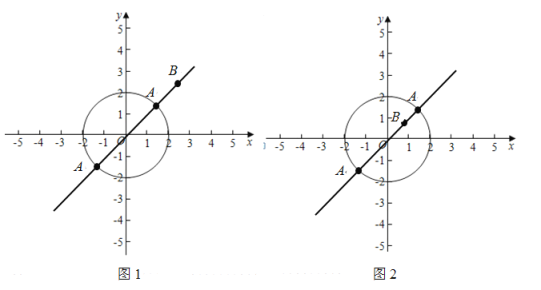
��m��Rʱ����B��Բ�ڣ���ͼ2��
ͬ���ɵã�AB�����ֵΪR+m����СΪR��m��
�ʴ�Ϊ��R+m��m��R��R+m��R��m��
��2�����ߵ�A��6��8����B����1��0����
��AO��10��BO��1��
��KA����10+2������10��2����4��
KB����2+1������2��1����2��
�ʴ�Ϊ4��2��
������P��ԲO��ʱ��KP��2R��4�����������⣻
����P��ԲO��ʱ��KP��2OP��2![]() ��
��
��OP��![]() ��
��
��P��ֱ��y��2x��1�ϣ�
��P��m��2m��1����
��m2+��2m��1��2��2��
��m��1��m����![]() ��
��
����P�ĺ�����Ϊ1��![]() ��
��
����![]() ��4��
��4��
���P��ԲO���ڲ���
����P����OΪԲ�ģ��뾶�ֱ�Ϊ![]() ��
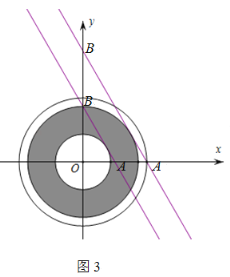
��![]() Χ�ɵ�Բ���ڣ����߽磩�����߶�AB��ͼ����Ӱ�����й����㣬��ͼ3��
Χ�ɵ�Բ���ڣ����߽磩�����߶�AB��ͼ����Ӱ�����й����㣬��ͼ3��
��![]() ��b��0������OΪԲ�ģ�
��b��0������OΪԲ�ģ�![]() Ϊ�뾶��Բ����ʱ��
Ϊ�뾶��Բ����ʱ��![]() ��
��![]() ����b��1��
����b��1��
��![]() ��b��0������OΪԲ�ģ�
��b��0������OΪԲ�ģ�![]() Ϊ�뾶��Բ����ʱ��
Ϊ�뾶��Բ����ʱ��![]() ��
��![]() ����b��2��
����b��2��
��b��ȡֵ��ΧΪ��1��b��2��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ������
������![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ��������
ͬʱ��������![]() ��
��![]() ���ٶ����յ�
���ٶ����յ�![]() �����˶�����
�����˶�����![]() ��
��![]() ���ٶ����յ�
���ٶ����յ�![]() �����˶�������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊ
�����˶�������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊ![]() ��
��

��1����![]() ʱ�����ı���
ʱ�����ı���![]() �������
�������
��2����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() Ϊ
Ϊ![]() ��
��
��3����![]() Ϊ��ֵʱ���Ե�
Ϊ��ֵʱ���Ե�![]() ��
��![]() ��
��![]() Ϊ������������ǵ��������Σ�
Ϊ������������ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ����x�ύ�ڵ㣨-3��0������x1��0������2��x1��3����y��ĸ����ύ�ڵ㣨0��-3�����Ϸ������н��ۣ���a��b��0����6a+c��0����9a+c��0����3a��b+1��������ȷ���۵ĸ���Ϊ�� ��
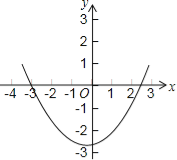
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˹�������籭��ȼ��ͬѧ�Ƕ������˶������飬ijѧУ������ס�������Ʒ�Ƶ�����ѧ��ʹ�ã���֪��1000 Ԫ��������������������1600Ԫ�������������������ͬ����������ĵ��۱���������ĵ�����30Ԫ��
��1����ס�������Ʒ�Ƶ�����ĵ��۸��Ƕ���Ԫ��
��2��ѧ֦��һ���Թ���ס�������Ʒ�Ƶ�����25�������ܷ��ò�����1610Ԫ����ô����ѧУ������ٸ�����Ʒ�Ƶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
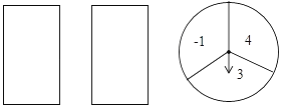
����Ŀ��С����鿨Ƭ����ת����Ϸ������������ֱ��������1����2�IJ�����Ƭ��������ȫ��ͬ��ת�̱�ƽ���ֳ�3����ȵ����Σ����ֱ�������֩�1��3��4����ͼ��ʾ����С�ưѿ�Ƭ���泯��ϴ�Ⱥ����������һ�ţ����¿�Ƭ�ϵ����֣�Ȼ��ת��ת�̣�ת��ֹͣ����ָ��������������֣���ָ���ڷָ����ϣ�����תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ���������б�����״ͼ�ķ�����ֻѡ����һ�֣������������֮��Ϊ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
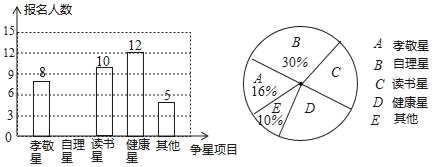
����Ŀ��ijСѧ��չ�������ǻ��ѧ�����Դ���������������������������������������Т����������ѡһ����Ŀ�μ����Ǿ�ѡ�����ݸ�Уһ�꼶ij��ѧ������������������������Ƴ�������������������ͳ��ͼ�������ͼ����Ϣ�ش��������⣺
��1���μӵ����ѧ�������� ���ˣ�
��2��������ͳ��ͼ����������
��3�����������ͳ��ͼ��������������Ӧ������Բ�ĽǶ�����
��4�����ݵ��������Թ��Ƹ�СѧȫУ3600��ѧ��������������������ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����л�����ʡ��̫ԭ��һ����ںӴ���(��ͼ1)����������߶Ȳ�ͬ���羶Ҳ��ͬ���������ֹ�ͨ�����ţ�������������������ߵĸֹ���ͼ2��ʾ���˸ֹ�(���ƿ��ɶ��κ�����ͼ��-������)��ͬһ��ֱƽ���ڣ��빰�����ڵ�ˮƽ���ཻ��A��B���㣬����Ϊ78��(����ߵ�O��AB�ľ���Ϊ78��)���羶Ϊ90��(��AB=90��)������ߵ�OΪ����ԭ�㣬��ƽ����AB��ֱ��Ϊ![]() �Ὠ��ƽ��ֱ������ϵ����������߸ֹ��ĺ�������ʽΪ( )
�Ὠ��ƽ��ֱ������ϵ����������߸ֹ��ĺ�������ʽΪ( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��ҵ��С����Ӧ������������ҵ���ĺ��٣���������С����Ϣ�������һ����Ʒ�꣮�õ깺��һ�ֽ��������е���Ʒ�������ۣ���Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ�Ϊÿ��60Ԫʱ��ÿ�¿�����300�����г����鷴ӳ�������۸�ʱ���ۼ�ÿ��1Ԫÿ��Ҫ����10�����ۼ�ÿ�½�1Ԫÿ��Ҫ����20����Ϊ�˻�ø���������ֽ���Ʒ�ۼ۵���Ϊx��Ԫ/������ÿ����Ʒ����Ϊy��������������Ϊw��Ԫ����
��1��ֱ��д��y��x֮��ĺ�����ϵʽ��
��2�����ȷ���ۼ۲���ʹ��������������������
��3��Ϊ��ʹÿ����������6000ԪӦ��ο����ۼۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������1���ಿ��ͬѧ����һ������Ϊ�����ʺ��Լ��Ŀ�ǰ��ѹ��ʽ���ĵ������ռ��������ݺ���ʦ����ѹ��ʽ��Ϊ���࣬��������ͼ1��ͼ2������������ͳ��ͼ�������ͼ�е���Ϣ����������⣮
��1��������1������ܵ����ͬѧ���ж�������
��2����ȫ����ͳ��ͼ������������ͳ��ͼ�е��������C������Ӧ��Բ�ĽǶ�����
��3����ϲ��������̸������5��ͬѧ������������������Ů������ʦ���5��ͬѧ����ѡ����ͬѧ���н�����ֱ��д��ѡȡ������ͬѧ����Ů���ĸ��ʣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com