练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
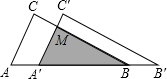
    如图所示，把△ABC沿AB边平移到△A′B′C′的位置，它们的重叠部分（即图中的阴影部分）的面积是△ABC的面积的一半，若AB=
    		2
    ，求此三角形移动的距离AA′．
    考点：相似三角形的判定与性质,平移的性质
    专题：
    分析：由题意可证明△BA′M∽△BAC，由面积比可求得
    BA′
    BA
    ，可求得A′B，可求得答案．
    解答：解：由平移可得A′C′∥AC，
    ∴△BA′M∽△BAC，
    ∴
    S△BA′M
    S△BAC
    =（
    BA′
    BA
    ）2=
    1
    2
    ，
    ∴
    BA′
    BA
    =
    1
    		2
    ，
    又∵AB=
    		2
    ，
    ∴BA′=1，
    ∴AA′=BA-BA′=
    		2
    -1．
    点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方，求得
    BA′
    BA
    是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    3个球队进行单循环比赛（参加比赛的每一个队都与其他所有队各赛一场），则总场数是
     
    ，4个队呢？
     
    ，n个队呢？
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    Rt△ABC中AB是斜边，AC=BC，点P是△ABC内一点，将△APC绕C逆时针旋转后能与△BDC完全重合，若PC=5，则PD的值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在扇形OAB中，∠AOB=105°，半径OA=10，将扇形OAB沿过点B的直线折叠，点O恰好落在弧AB上的点D处，折痕BC交OA于点C，则图中阴影部分面积为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

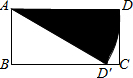    如图，在矩形ABCD中，AB=1，AD=2，将AD边绕点A顺时针旋转，使点D恰好落在BC边上的D′处，则阴影部分的扇形面积为（　　）
    A、π
    B、
    π
    2
    C、
    π
    3
    D、
    π
    4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，DE∥BC，DF∥AB，∠1=70°，求∠D、∠2和∠3的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将多边形切去一角后得到的多边形的内角和为900°，则原多边形的边数为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，Rt△ABC和Rt△DCE的斜边长相等，其中∠ACB=∠CED=90°，∠A=45°，∠CDE=30°，∠BCE=15°，连接DB，则∠EDB的度数为（　　）
    A、10°B、20°
    C、7.5°D、15°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知圆O的直径为6，CD为圆O的直径，且CD⊥AB，∠D=15°．则OE的长为（　　）
    A、3
    B、3
    		3
    C、
    3
    2
    D、
    3
    2
    		3

    查看答案和解析>>

    同步练习册答案