
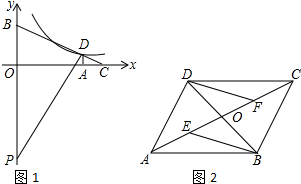
分析 (1)①根据正切值,可得PD的斜率,根据直线垂直,可得BD的斜率,可得直线BC,根据函数值为0,可得C点坐标;
②根据自变量的值,可得D点坐标,根据待定系数法,可得函数解析式;
(2)①由DF与BE平行,得到两对内错角相等,再由O为AC的中点,得到OA=OC,又AE=CF,得到OE=OF,利用AAS即可得证;
②若OD=$\frac{1}{2}$AC,则四边形ABCD为矩形,理由为:由OD=$\frac{1}{2}$AC,得到OB=$\frac{1}{2}$AC,即OD=OA=OC=OB,利用对角线互相平分且相等的四边形为矩形即可得证
解答 解:Rt△PBD的斜边PB落在y轴上,
∴BD⊥PD,
kPD=cot∠BPD=$\frac{1}{tan∠BPD}$,
kBD•kPD=-1,
kBD=-$\frac{1}{2}$,
直线BD的解析式是y=-$\frac{1}{2}$x+3,
当y=0时,-$\frac{1}{2}$x+3=0,
x=6,
C点坐标是(6,0);
②当x=4时,y=-$\frac{1}{2}$×4+3=1,
∴D(4,1).
点D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,
∴k=4×1=4,
∴反比例函数的解析式为 y=$\frac{4}{x}$.
(2)①证明:∵DF∥BE,
∴∠FDO=∠EBO,∠DFO=∠BEO,
∵O为AC的中点,
∴OA=OC,
∵AE=CF,
∴OA-AE=OC-CF,
即OE=OF,
在△BOE和△DOF中,
$\left\{\begin{array}{l}{∠FDO=∠EBO}\\{∠DFO=∠BEO}\\{OE=OF}\end{array}\right.$,
∴△BOE≌△DOF(AAS);
②若OD=$\frac{1}{2}$AC,则四边形ABCD是矩形,理由为:
证明:∵△BOE≌△DOF,
∴OB=OD,
∵OD=$\frac{1}{2}$AC,
∴OA=OB=OC=OD,且BD=AC,
∴四边形ABCD为矩形;
点评 本题考查了反比例函数与一次函数的交点问题及全等三角形的判定与性质,矩形的判定与性质,以及平行线的性质,先求出PD的斜率求出BD的斜率,求出直线BD,再求出点的坐标;熟练掌握全等三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
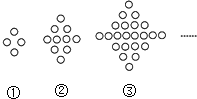 如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )
如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )| A. | 46 | B. | 70 | C. | 94 | D. | 190 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
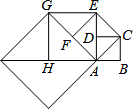 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a2013=21006.
如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a2013=21006.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
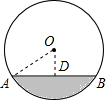 如图,小明郑处的铅球在场地上砸出一个小坑,小坑的直径AB为10cm,深为2cm(小坑的最大深度为2cm),则该铅球的半径OA为$\frac{29}{4}$cm.
如图,小明郑处的铅球在场地上砸出一个小坑,小坑的直径AB为10cm,深为2cm(小坑的最大深度为2cm),则该铅球的半径OA为$\frac{29}{4}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
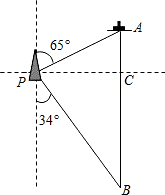 如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海伦所在的B处距离灯塔P有多远?(sin65°≈0.91,cos65°≈0.42,sin34°≈0.56,cos34°≈0.83)
如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海伦所在的B处距离灯塔P有多远?(sin65°≈0.91,cos65°≈0.42,sin34°≈0.56,cos34°≈0.83)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
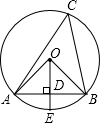 如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )
如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )| A. | ∠ACB=∠AOE | B. | AD=BD | C. | S△AOB=$\frac{1}{2}$S△ABC | D. | AE=BE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com