
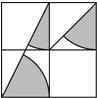
 如图,方格纸中4个小正方形的边长均为1,求图中阴影部分三个小扇形的面积和以及周长的和(结果保留π).
如图,方格纸中4个小正方形的边长均为1,求图中阴影部分三个小扇形的面积和以及周长的和(结果保留π).科目:初中数学 来源: 题型:
| A-C | C-D | E-D | F-E | G-F | B-G |
| 90米 | 80米 | -60米 | 50米 | -70米 | 40米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
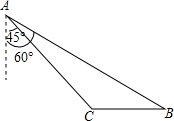 如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据:
如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据:| 2 |
| 3 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
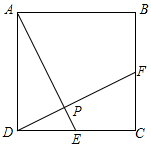 正方形ABCD中,E,F分别为边DC,BC上的点,连接AE,DF且AE⊥DF于点P.
正方形ABCD中,E,F分别为边DC,BC上的点,连接AE,DF且AE⊥DF于点P.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、y=(x-2)2+3 |
| B、y=(x+2)2-3 |
| C、y=(x+2)2+3 |
| D、y=-(x+2)2+3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com