
分析 (1)π的十分位为1,应该舍去,所以精确到个位是3;
(2)$\frac{4}{3}$x为整数,设这个整数为k,易得这个整数应在应在k-$\frac{1}{2}$和k+$\frac{1}{2}$之间,包括k-$\frac{1}{2}$,不包括k+$\frac{1}{2}$,求得整数k的值即可求得x的非负实数的值;
(3)易得二次函数的对称轴,那么可求得二次函数的函数值在相应的自变量的范围内取值,进而求得相应的a的个数;利用所给关系式易得$\sqrt{k}$的正整数个数为2n,由此得证.
解答 (1)解:因为π≈3.14,所以四舍五入后的个位数为3.
故答案是:3;
(2)解:∵x≥0,$\frac{4}{3}$x为整数,设$\frac{4}{3}$x=k,k为整数,
则x=$\frac{3}{4}$k,
∴<$\frac{3}{4}$k>=k,
∴k-$\frac{1}{2}$≤$\frac{3}{4}$k≤k+$\frac{1}{2}$,k≥0,
∵O≤k≤2,
∴k=0,1,2,
∴x=0,$\frac{3}{4}$,$\frac{3}{2}$.
(3)证明:∵函数y=x2-x+$\frac{1}{4}$=(x-$\frac{1}{2}$)2,n为整数,
当n≤x<n+1时,y随x的增大而增大,
∴(n-$\frac{1}{2}$)2≤y<(n+1-$\frac{1}{2}$)2,即(n-$\frac{1}{2}$)2≤y<(n+$\frac{1}{2}$)2,①
∴n2-n+$\frac{1}{4}$≤y<n2+n+$\frac{1}{4}$,
∵y为整数,
∴y=n2-n+1,n2-n+2,n2-n+3,…,n2-n+2n,共2n个y,
∴a=2n,②
∵k>0,<$\sqrt{k}$>=n,
则n-$\frac{1}{2}$≤$\sqrt{k}$<n+$\frac{1}{2}$,
∴(n-$\frac{1}{2}$)2≤k<(n+$\frac{1}{2}$)2,③
比较①,②,③得:a=b=2n.
点评 本题考查了二次函数综合题.解决本题的关键是理解:对非负实数x“四舍五入”到个位的值记为<x>,即:当n为非负整数时,如果n-$\frac{1}{2}$≤x<n+$\frac{1}{2}$,则<x>=n.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
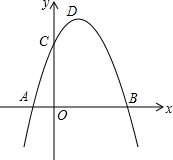 如图,已知抛物线 y=-x2+mx+4m 的图象与x轴交于A、B两点,与y轴交于点C(0,8).
如图,已知抛物线 y=-x2+mx+4m 的图象与x轴交于A、B两点,与y轴交于点C(0,8).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
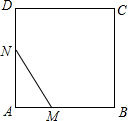 如图,已知线段AB长度是4,以AB为边作正方形ABCD,动点M,N在正方形的边上运动,且MN=3,如果点M从点A出发,沿着A→B→C→D→A的路线,向点A运动,则点M从点A运动一周回到点A的运动过程中,MN的中点P所经过的路线长度是3π+4.
如图,已知线段AB长度是4,以AB为边作正方形ABCD,动点M,N在正方形的边上运动,且MN=3,如果点M从点A出发,沿着A→B→C→D→A的路线,向点A运动,则点M从点A运动一周回到点A的运动过程中,MN的中点P所经过的路线长度是3π+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
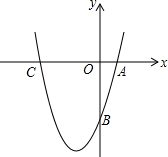 如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.
如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
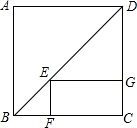 如图,已知正方形ABCD的一条对角线长为10$\sqrt{2}$cm,矩形EFCG的3个顶点分别在△BCD的边上.则矩形EFCG的周长是20cm.
如图,已知正方形ABCD的一条对角线长为10$\sqrt{2}$cm,矩形EFCG的3个顶点分别在△BCD的边上.则矩形EFCG的周长是20cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com