
【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.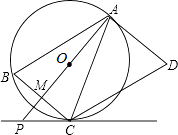
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若AB=9,BC=6.求PC的长.
【答案】
(1)解:PC与圆O相切,理由为:
过C点作直径CE,连接EB,如图, 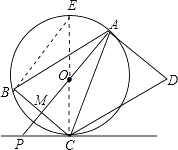
∵CE为直径,
∴∠EBC=90°,即∠E+∠BCE=90°,
∵AB∥DC,
∴∠ACD=∠BAC,
∵∠BAC=∠E,∠BCP=∠ACD.
∴∠E=∠BCP,
∴∠BCP+∠BCE=90°,即∠PCE=90°,
∴CE⊥PC,
∴PC与圆O相切
(2)解:∵AD是⊙O的切线,切点为A,
∴OA⊥AD,
∵BC∥AD,
∴AM⊥BC,
∴BM=CM= ![]() BC=3,
BC=3,
∴AC=AB=9,
在Rt△AMC中,AM= ![]() =6
=6 ![]() ,
,
设⊙O的半径为r,则OC=r,OM=AM﹣r=6 ![]() ﹣r,
﹣r,
在Rt△OCM中,OM2+CM2=OC2,即32+(6 ![]() ﹣r)2=r2,解得r=
﹣r)2=r2,解得r= ![]() ,
,
∴CE=2r= ![]() ,OM=6
,OM=6 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴BE=2OM= ![]() ,
,
∵∠E=∠MCP,
∴Rt△PCM∽Rt△CEB,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴PC= ![]() .
.
【解析】(1)由CE为直径,得到∠E+∠BCE=90°,由AB∥DC,得到内错角相等即∠ACD=∠BAC,根据圆周角性质从而得到∠E=∠BCP,得到结论PC与圆O相切;(2)根据切线和平行线的性质,得到BM=CM=![]() BC,根据中垂线的性质得到AC=AB,根据勾股定理求出AM的长,求出⊙O的半径,由∠E=∠MCP,得到Rt△PCM∽Rt△CEB,从而求出PC的长.
BC,根据中垂线的性质得到AC=AB,根据勾股定理求出AM的长,求出⊙O的半径,由∠E=∠MCP,得到Rt△PCM∽Rt△CEB,从而求出PC的长.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;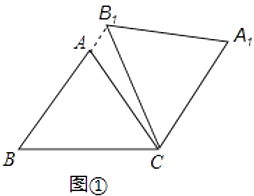
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.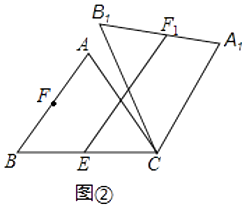
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某油箱容量为60L的汽车,加满汽油后行驶了100km时,油箱中的汽油大约消耗了![]() ,如果加满汽油后汽车行驶的路程为x(km),油箱中剩油量为y(L),则y与x之间的函数解析式和自变量取值范围分别是( )
,如果加满汽油后汽车行驶的路程为x(km),油箱中剩油量为y(L),则y与x之间的函数解析式和自变量取值范围分别是( )
A. y=0.12x,x>0
B. y=60-0.12x,x>0
C. y=0.12x,0≤x≤500
D. y=60-0.12x,0≤x≤500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示.现将△ABC平移,使得点A移至图中的点A'的位置.
(1)平移后所得△ABC的顶点B的坐标为 ,C的坐标为 ;
(2)平移过程中△ABC扫过的面积为 ;
(3)将直线AB以每秒1个单位长度的速度向右平移,则平移 秒时该直线恰好经过点C.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.732)
≈1.732)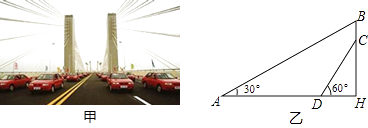
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]()

(1)画出![]() 的
的![]() 边上的高CH;
边上的高CH;
(2)将![]() 平移到
平移到![]() (点
(点![]() 和点
和点![]() 对应,点
对应,点![]() 和点
和点![]() 对应,点
对应,点![]() 和点
和点![]() 对应),若点
对应),若点![]() 的坐标为
的坐标为![]() ,请画出平移后的
,请画出平移后的![]() ;
;
(3)若![]() ,
,![]() 为平面内一点,且满足
为平面内一点,且满足![]() 与
与![]() 全等,请直接写出点
全等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,AC和BD相交于点O,OA=OC,OB=OD,求证:DC∥AB.
(2)如图2,在⊙O中,直径AB=6,AB与弦CD相交于点E,连接AC、BD,若AC=2,求cosD的值.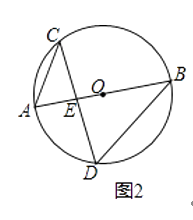
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P是AB的中点,![]() 的延长线于点E,连接AE,过点A作
的延长线于点E,连接AE,过点A作![]() 交DP于点F,连接BF、
交DP于点F,连接BF、![]() 下列结论中:
下列结论中:![]() ≌
≌![]() ;
;![]() ;
;![]() 是等边三角形;
是等边三角形;![]() ;
;![]() 其中正确的是
其中正确的是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com