考点:分式方程的解
专题:
分析:先将原方程化为
=0,再分三种情况进行讨论:(1)若x≠0且x≠2,则2x
2-2x+4+a=0,由原分式方程恰有一个实根,得出△=(-2)
2-4×2×(4+a)=-28-8a=0,依此求出a的值;(2)若方程2x
2-2x+4+a=0,有一个根为x=0,代入求出a=-4,再解方程即可;(3)若方程2x
2-2x+4+a=0,有一个根为x=2,代入求出a=-8,再解方程即可.
解答:解:原方程化为
=0.
(1)若x≠0且x≠2,则2x
2-2x+4+a=0,
∵原分式方程恰有一个实根,
∴△=0,即△=(-2)
2-4×2×(4+a)=-28-8a=0,
则a=-
,
于是x
1=x
2=
,
但a取整数,则舍去;
(2)若方程2x
2-2x+4+a=0,有一个根为x=0,则a=-4,
这时原方程为
+
+
=0,
去分母得2x
2-2x=0,
解得x=0,x=1,
显然x=0是增根,x=1是原分式方程的根;
(3)若方程2x
2-2x+4+a=0,有一个根为x=2,则a=-8,
这时,原方程为
+
+
=0,
去分母,得2x
2-2x-4=0,
解得x=2,x=-1,
显然x=2是增根,x=-1是原分式方程的根;
经检验当a=-4时,原方程恰有一个实根x=1;当a=-8时,原方程恰有一个实根x=-1.
点评:本题考查了分式方程的解,理解分式方程产生增根的原因进而分情况讨论是解题的关键.




 如图,△ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE,设△BOE、△BOC、△COD和四边形AEOD的面积,分别为S1、S2、S3和S4.
如图,△ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE,设△BOE、△BOC、△COD和四边形AEOD的面积,分别为S1、S2、S3和S4.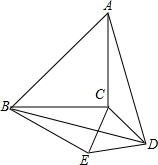 如图,以等腰直角三角形ABC的斜边AB为边向顶点C的同侧等边△ABD,连接DC,以DC为边作等边△DCE,B、E在CD的同侧,若BC=2,则BE=
如图,以等腰直角三角形ABC的斜边AB为边向顶点C的同侧等边△ABD,连接DC,以DC为边作等边△DCE,B、E在CD的同侧,若BC=2,则BE=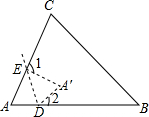 如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE重叠压平,A与A′重合,若∠A=60°,则∠1+∠2=( )
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE重叠压平,A与A′重合,若∠A=60°,则∠1+∠2=( )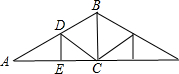 如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,DE=2m,则AB的长为( )
如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,DE=2m,则AB的长为( )