
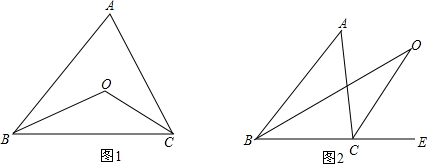
分析 (1)如图1,根据角平分线的定义得到∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,在根据三角形内角和定理得∠BOC=180°-∠1-∠2,则∠BOC=180°-$\frac{1}{2}$(∠ABC+∠ACB),由于∠ABC+∠ACB=180°-∠A,所以∠BOC=90°+$\frac{1}{2}$∠A;
(2)根据角平分线的定义得∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACE,再利用三角形外角性质得∠2=∠1+∠O,∠ACE=∠ABC+∠A,由于$\frac{1}{2}$∠ACE=$\frac{1}{2}$∠ABC+∠0,则∠A=2∠O,即∠O=$\frac{1}{2}$∠A.
解答 (1)证明: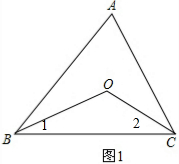 如图1,
如图1,
∵BO、CO是△ABC的角平分线,
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,
∵∠BOC=180°-∠1-∠2,
∴∠BOC=180°-$\frac{1}{2}$(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A,
∴∠BOC=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A;
(2)解:∠O=$\frac{1}{2}$∠A.理由如下:
如图2,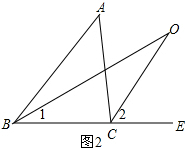 ∵BO是△ABC的平分线,
∵BO是△ABC的平分线,
∴∠1=$\frac{1}{2}$∠ABC,
∵CO是∠ACE的平分线,
∴∠2=$\frac{1}{2}$∠ACE,
∵∠2=∠1+∠O,
∴$\frac{1}{2}$∠ACE=$\frac{1}{2}$∠ABC+∠0,
即∠ACE=∠ABC+2∠0,
∵∠ACE=∠ABC+∠A,
∴∠A=2∠O,
即∠O=$\frac{1}{2}$∠A.
点评 本题考查了三角形内角和定理:三角形内角和是180°.利用三角形内角和可直接根据两已知角求第三个角或依据三角形中角的关系,用代数方法求三个角,也可在直角三角形中,已知一锐角可利用两锐角互余求另一锐角.也考查了三角形外角性质.


科目:初中数学 来源: 题型:填空题
 用长为8m的铝合金条做一个如图所示的矩形窗框,设水平的一边长为xcm,窗户的透光面积为ym2,那么y与x之间的函数表达式为y=-$\frac{3}{2}$x2+4x.
用长为8m的铝合金条做一个如图所示的矩形窗框,设水平的一边长为xcm,窗户的透光面积为ym2,那么y与x之间的函数表达式为y=-$\frac{3}{2}$x2+4x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
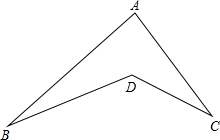 如图.点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.
如图.点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 经过一点有且只有一条直线与已知直线垂直 | |
| B. | 圆锥的截面一定是圆 | |
| C. | 过两点有且只有一条直线 | |
| D. | 如a∥b,b∥c,则a∥c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com