
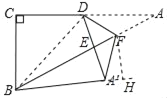
【题目】如图,在Rt△ABC中,∠C=90°,AC=4![]() ,BC=4,点D是AC的中点,点F是边AB上一动点,沿DF所在直线把△ADF翻折到△A′DF的位置,若线段A′D交AB于点E,且△BA′E为直角三角形,则BF的长为_____.
,BC=4,点D是AC的中点,点F是边AB上一动点,沿DF所在直线把△ADF翻折到△A′DF的位置,若线段A′D交AB于点E,且△BA′E为直角三角形,则BF的长为_____.

【答案】6或![]()
【解析】
由三角函数得出∠A=30°,由直角三角形的性质得出AB=2BC=8,由折叠的性质得出DA=DC=![]() ,FA′=FA,∠DA′F=∠A=30°,设BF=x,则AF=8﹣x,FA′=8﹣x,①当∠BEA′=90°时,由三角函数得出AE=3,得出EF=3﹣(8﹣x)=x﹣5,由直角三角形的性质得出方程,解方程即可;
,FA′=FA,∠DA′F=∠A=30°,设BF=x,则AF=8﹣x,FA′=8﹣x,①当∠BEA′=90°时,由三角函数得出AE=3,得出EF=3﹣(8﹣x)=x﹣5,由直角三角形的性质得出方程,解方程即可;
②当∠BA'E=90°时,作FH⊥BA',交BA'的延长线于H,连接BD,证明Rt△BDA'≌Rt△BDC,得出BA′=BC=4,求出∠FA'H=60°,在Rt△BFH中,由勾股定理得出方程,解方程即可.
解:∵∠C=90°,AC=![]() ,BC=4,
,BC=4,
∴tanA=![]() ,
,
∴∠A=30°,
∴AB=2BC=8,
∵点D是AC的中点,沿DF所在直线把△ADF翻折到△A′DF的位置,线段A′D交AB于点E,
∴DA=DC=![]() ,FA′=FA,∠DA′F=∠A=30°,
,FA′=FA,∠DA′F=∠A=30°,
设BF=x,则AF=8﹣x,FA′=8﹣x,
①当∠BEA′=90°时,在Rt△ADE中,cosA=![]() ,
,
∴AE=![]() ×cos30°=3,
×cos30°=3,
∴EF=3﹣(8﹣x)=x﹣5,
在Rt△A'FE中,∵∠FA'E=30°,
∴FA'=2FE,即8﹣x=2(x﹣5),
解得x=6,即BF=6;
②当∠BA'E=90°时,作FH⊥BA',交BA'的延长线于H,连接BD,如图所示:
在Rt△BDA'和△BDC中,![]() ,
,
∴Rt△BDA'≌Rt△BDC(HL),
∴BA′=BC=4,
∵∠BA'F=∠BA'E+∠FA'E=90°+30°=120°,
∴∠FA'H=60°,
在Rt△FHA'中,A′H=![]() A′F=
A′F=![]() (8﹣x),FH=
(8﹣x),FH=![]() A′H=
A′H=![]() (8﹣x),
(8﹣x),
在Rt△BFH中,∵FH2+BH2=BF2,
∴![]() (8﹣x)2+[
(8﹣x)2+[![]() (8﹣x)+4]2=x2,
(8﹣x)+4]2=x2,
解得:x=![]() ,即BF=
,即BF=![]() .
.
综上所述,BF的长为6或![]() .
.
故答案为:6或![]() .
.


科目:初中数学 来源: 题型:
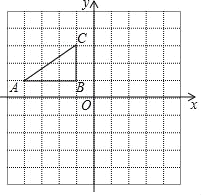
【题目】如图,在平面直角坐标系中,小正方形格子的边长为1,Rt△ABC三个顶点都在格点上,请解答下列问题:
(1)写出A,C两点的坐标;
(2)画出△ABC关于原点O的中心对称图形△A1B1C1;
(3)画出△ABC绕原点O顺时针旋转90°后得到的△A2B2C2,并直接写出点C旋转至C2经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
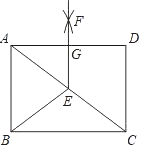
【题目】如图,AC是矩形ABCD的一条对角线,E是AC中点,连接BE,再分别以A,D为圆心,大于![]() 的长为半径作弧,两弧相交于点F,连接EF交AD于点G.若AB=3,BC=4,则四边形ABEG的周长为( )
的长为半径作弧,两弧相交于点F,连接EF交AD于点G.若AB=3,BC=4,则四边形ABEG的周长为( )
A. 8B. 8.5C. 9D. 9.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店用4000元购进一批足球,全部售完后,又用3600元再次购进同样的足球,但这次每个足球的进价是第一次进价的1.2倍,且数量比第一次少了10个.
(1)求第一次每个足球的进价是多少元?
(2)若第二次进货后按150元/个的价格销售,当售出10个后,根据市场情况,商店决定对剩余的足球全部按同一标准一次性打折售完,但要求这次的利润不少于450元,问该商店最低可打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对博鳌论坛会的了解情况,某中学随机抽取了部分学生进行问卷调查,将调查结果记作“![]() 非常了解,
非常了解,![]() 了解,
了解,![]() 了解较少,
了解较少,![]() 不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
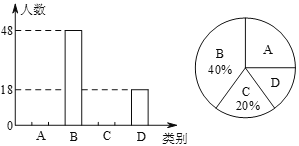
(1)此次共调查了______名学生;扇形统计图中![]() 所在的扇形的圆心角度数为______;
所在的扇形的圆心角度数为______;
(2)将条形统计图补充完整;
(3)若该校共有1600名学生,请你估计对博鳌论坛会的了解情况为“非常了解”的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
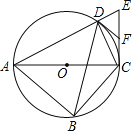
(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图![]() 所示,点
所示,点![]() 为矩形
为矩形![]() 边
边![]() 的中点,在矩形
的中点,在矩形![]() 的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员
的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路线匀速行进,到达点
的路线匀速行进,到达点![]() .设运动员
.设运动员![]() 的运动时间为
的运动时间为![]() ,到监测点的距离为
,到监测点的距离为![]() .现有
.现有![]() 与
与![]() 的函数关系的图象大致如图
的函数关系的图象大致如图![]() 所示,则这一信息的来源是( ).
所示,则这一信息的来源是( ).


A. 监测点![]() B. 监测点
B. 监测点![]() C. 监测点
C. 监测点![]() D. 监测点
D. 监测点![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数![]() (k≠0)的图象恰好经过点C和点D,则k的值为( )
(k≠0)的图象恰好经过点C和点D,则k的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,BC=10,AB⊥AC,点P从点B出发沿着B→A→C的路径运动,同时点Q从点A出发沿着A→C→D的路径以相同的速度运动,当点P到达点C时,点Q随之停止运动,设点P运动的路程为x,y=PQ2,下列图象中大致反映y与x之间的函数关系的是( )
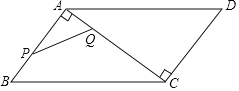
A. 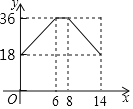 B.
B. 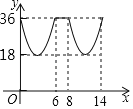
C. 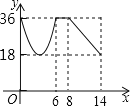 D.
D. 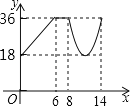
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com