
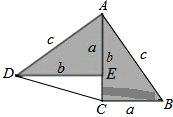
 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.科目:初中数学 来源: 题型:
| A、②③④ | B、③④⑤ |
| C、②③ | D、①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
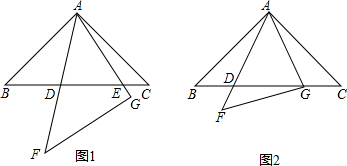
 将连续正整数按图所示的规律排列,观察图表并回答下列问题:
将连续正整数按图所示的规律排列,观察图表并回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
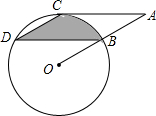 如图,点B、C、D都在⊙O上,过点C的⊙O的切线交OB延长线于点A,C连接CD、BD,若∠CDB=∠OBD=30°,OB=6cm.
如图,点B、C、D都在⊙O上,过点C的⊙O的切线交OB延长线于点A,C连接CD、BD,若∠CDB=∠OBD=30°,OB=6cm.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
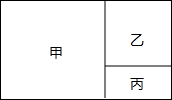 如图,是我市一块长方形土地,政府统一规划,把地分成甲、乙、丙三部分,甲和乙为正方形,现计划甲建设住宅区,乙建设一座标准化的中学,丙地建成植物园,若已知这块地的宽为120米,丙地的面积为3200平方米,请你计算出这块地的长是多少?
如图,是我市一块长方形土地,政府统一规划,把地分成甲、乙、丙三部分,甲和乙为正方形,现计划甲建设住宅区,乙建设一座标准化的中学,丙地建成植物园,若已知这块地的宽为120米,丙地的面积为3200平方米,请你计算出这块地的长是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com