
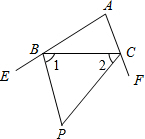
 如图,BP,CP分别是∠CBE,∠BCF的平分线,求出∠P与∠A的等量关系.
如图,BP,CP分别是∠CBE,∠BCF的平分线,求出∠P与∠A的等量关系. 分析 如图,设∠ABC=α,∠ACB=β;首先运用α、β表示出∠1+∠2,进而求出∠P;其次运用α、β表示出∠A,从而探究出∠P与∠A之间的等量关系.
解答  解:如图,设∠ABC=α,∠ACB=β;∵
解:如图,设∠ABC=α,∠ACB=β;∵
BP,CP分别是∠CBE,∠BCF的平分线,
∴∠1=$\frac{180°-α}{2}$,∠2=$\frac{180°-β}{2}$,
∴∠1+∠2=180°-$\frac{1}{2}$(α+β),
∴∠P=180°-[180°-$\frac{1}{2}$(α+β)]=$\frac{1}{2}$(α+β);
∵∠A=180°-(α+β),
∴∠P=90°-$\frac{1}{2}$∠A.
点评 该题主要考查了三角形的内角和定理、外角的性质等知识点及其应用问题;解题的关键是能够灵活运用三角形的内角和定理、外角的性质等知识点来分析、判断、解答.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)2=a2+b2 | B. | (a-b)2=a2-b2 | C. | (x-4)(x+4)=x2-4 | D. | (a+b)2=a2+b2+2ab |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com