
 如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,[即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…]且每秒运动一个单位长度,那么2015秒时,这个粒子所处位置为(9,44).
如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,[即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…]且每秒运动一个单位长度,那么2015秒时,这个粒子所处位置为(9,44). 分析 该题是点的坐标规律,通过对部分点分析,发现实质上是数列问题.设粒子运动到A1,A2,…An时所用的间分别为a1,a2,…an,则a1=2,a2=6,a3=12,a4=20,…,由an-an-1=2n,则
a2-a1=2×2,
a3-a2=2×3,
a4-a3=2×4,
…,
an-an-1=2n,
以上相加得到an-a1的值,进而求得an来解.
解答 解:由题意,
设粒子运动到A1,A2,…,An时所用的间分别为a1,a2,…,an,
则a1=2,a2=6,a3=12,a4=20,…,an-an-1=2n,
a2-a1=2×2,
a3-a2=2×3,
a4-a3=2×4,
…,
an-an-1=2n,
相加得:
an-a1=2(2+3+4+…+n)=n2+n-2,
∴an=n(n+1).
44×45=1980,故运动了1980秒时它到点A44(44,44);
又由运动规律知:A1,A2,…,An中,奇数点处向下运动,偶数点处向左运动.
故达到A44(44,44)时向左运动35秒到达点(9,44),
即运动了2015秒.所求点应为(9,44).
故答案为:(9,44)
点评 本题考查了平面直角坐标系内点的运动规律,分析粒子在第一象限的运动规律得到数列{an}通项的递推关系式an-an-1=2n是本题的突破口,本题对运动规律的探索可知知:A1,A2,…An中,奇数点处向下运动,偶数点处向左运动,找到这个规律是解题的关键.


科目:初中数学 来源: 题型:解答题
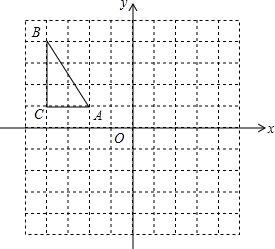 在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给的平面直角坐标系中按要求作图并完成填空:
在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给的平面直角坐标系中按要求作图并完成填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
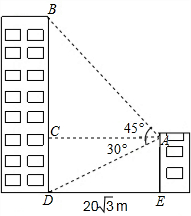 小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20$\sqrt{3}$米.
小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20$\sqrt{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x-y=20}\\{50x+50y=120}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=20}\\{\frac{5}{6}x+50y=120}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{50x-50y=20}\\{50x+50y=120}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{5}{6}x-\frac{5}{6}y=20}\\{\frac{5}{6}x+\frac{5}{6}y=120}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com