
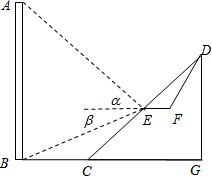
 如图,高36米的楼房AB正对着斜坡CD,点E在斜坡CD的中点处,已知斜坡的坡角(即∠DCG)为30°,AB⊥BC.
如图,高36米的楼房AB正对着斜坡CD,点E在斜坡CD的中点处,已知斜坡的坡角(即∠DCG)为30°,AB⊥BC.分析 (1)延长FE交AB于M,设ME=x,根据直角三角形函数得出AM=tanα•x,BM=tanβ•x,然后根据tanα•x+tanβ•x=36,即可求得EM的长,然后通过余弦函数即可求得AE;
(2)根据BM=NG=DN,得到DN的长,然后解直角三角形函数求得EN和FN,进而求得EF和DF的长,然后根据题意列出方程,解方程即可求得.
解答 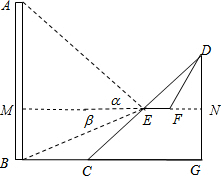 解:(1)延长FE交AB于M,
解:(1)延长FE交AB于M,
∵EF∥BC,
∴MN⊥AB,MN⊥DG,
设ME=x,
∴AM=tanα•x,BM=tanβ•x,
∵AB=36,
∴tanα•x+tanβ•x=36,
∴tan37°x+tan24°x=36,
0.75x+0.45x=36,
解得x=30,
∴AE=$\frac{EM}{cos37°}$=$\frac{30}{0.80}$≈37.5(米);
(2)延长EF交DG于N,
∵GN=BM=tan24°•30=13.5,DE=CE,EF∥BC,
∴DN=GN=13.5(米),
∵∠DCG=30°,
∴∠DEN=30°,
∴EN=DN•cot30°=13.5×$\sqrt{3}$,
∵$\frac{DN}{FN}$=$\frac{\sqrt{3}}{1}$,
∴∠DFN=60°,
∴∠EDF=30°,FN=DN•cot60°=13.5×$\frac{\sqrt{3}}{3}$,
∴DF=EF=EN-FN=13.5×$\frac{2\sqrt{3}}{3}$,
∴EF+DF=27×$\frac{2\sqrt{3}}{3}$=18$\sqrt{3}$,
设施工队原计划平均每天修建y米,
根据题意得,$\frac{18\sqrt{3}}{y}$=$\frac{18\sqrt{3}}{1.5t}$+2,
解得y=3$\sqrt{3}$(米),
经检验,是方程的根,
答:施工队原计划平均每天修建3$\sqrt{3}$米.
点评 本题考查了解直角三角形的应用,题目中涉及到了仰俯角和坡度角的问题,解题的关键是构造直角三角形.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+49b}{100}$ | B. | $\frac{51a+b}{100}$ | C. | $\frac{a+b}{100}$ | D. | $\frac{51a+49b}{100}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
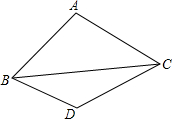 如图,在△ABC中,AB=AC,点D为△ABC外一点,且AC=CD,∠CBD=30°,求证:∠BDC=180°-$\frac{1}{2}$∠BAC.
如图,在△ABC中,AB=AC,点D为△ABC外一点,且AC=CD,∠CBD=30°,求证:∠BDC=180°-$\frac{1}{2}$∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com