
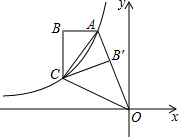
 如图,双曲线y=
如图,双曲线y=| k |
| x |
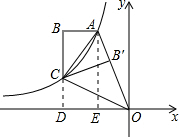 解:延长BC,与x轴交于点D,可得CD⊥x轴,作AE⊥x轴,如图所示,
解:延长BC,与x轴交于点D,可得CD⊥x轴,作AE⊥x轴,如图所示,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| k |
| 4 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
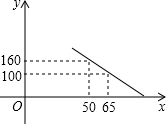 大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电.通过试销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.求y与x的函数表达式.
大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电.通过试销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.求y与x的函数表达式.查看答案和解析>>
科目:初中数学 来源: 题型:
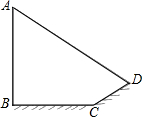 如图,小明想测量一棵大树AB的高度,发现大树的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与地面成45°,且此时测得1m竖杆的影子长是2m,求大树的高度是多少米?
如图,小明想测量一棵大树AB的高度,发现大树的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与地面成45°,且此时测得1m竖杆的影子长是2m,求大树的高度是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知Rt△ABC中,BC=9,AB=12,过点A作AE⊥AB,且AE=16,连接BE交AC于点P.
如图,已知Rt△ABC中,BC=9,AB=12,过点A作AE⊥AB,且AE=16,连接BE交AC于点P.查看答案和解析>>
科目:初中数学 来源: 题型:
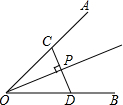 如图,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.
如图,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.| A、小于 | B、大于 |
| C、等于 | D、不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com