
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,由点
上,由点![]() 向点
向点![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时,停止运动.以点
重合时,停止运动.以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 在
在![]() 上且在矩形
上且在矩形![]() 外,
外,![]() .
.
(1)当![]() 时,
时,![]() __________,扇形
__________,扇形![]() 的面积=__________,点
的面积=__________,点![]() 到
到![]() 的最短距离=__________.
的最短距离=__________.
(2)![]() 与
与![]() 相切时,求
相切时,求![]() 的长?
的长?
(3)如图![]() 与
与![]() 交于点
交于点![]() 、
、![]() ,当
,当![]() 时,求
时,求![]() 的长?
的长?
(4)请从下面两问中,任选一道进行作答.
①当![]() 与
与![]() 有两个公共点时,直接写出
有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
②直接写出点![]() 的运动路径长以及
的运动路径长以及![]() 的最短距离.
的最短距离.
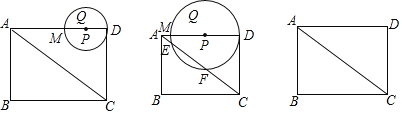
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)4;(4)①
;(3)4;(4)①![]() ,或
,或![]() ;②
;②![]() ,
,![]()
【解析】
(1)根据已知直接可求;
(2)⊙P与AC相切时,设切点为点H,连接PH,则PH⊥AC,在Rt△ADC中,AB=6,BC=8,得AC=10;在Rt△ADC中,sin∠DAC=![]() ,设⊙P半径为x,则PH=PD=x,AP=8-x,在Rt△AHP中,sin∠PAH=
,设⊙P半径为x,则PH=PD=x,AP=8-x,在Rt△AHP中,sin∠PAH=![]() =
=![]() ,可求x=3,在Rt△PDC中,CD=6,PD=3,求得PC=
,可求x=3,在Rt△PDC中,CD=6,PD=3,求得PC=![]() ;
;
(3)过点P作PH⊥AC,连接PF;则∠PHA=∠ADC=90°,可证△AHP∽△ADC,设⊙P半径为x,则PF=PD=x,AP=8-x,则PH=![]() (8-x),在⊙P中,FH⊥AC,EF=6.4,HF=3.2,在Rt△PHF中,(
(8-x),在⊙P中,FH⊥AC,EF=6.4,HF=3.2,在Rt△PHF中,(![]() (8x))2+3.22=x2,求得PD=4;
(8x))2+3.22=x2,求得PD=4;
(4)①作PM⊥AC于M,作PN⊥BC于N,易知PM=PD时,⊙P与AC相切,与△ABC只有一个公共点,PM<PD时⊙P与△ABC没有公共点;当PN=PD时,⊙P与BC相切,⊙P与△ABC有三个公共点,当PB=PD时,⊙P与△ABC有三个公共点;当PB<PD≤AD时,⊙P与△ABC有且只有两个公共点;故3<PD<6或![]() <PD≤8;②由∠QPD=120°,PQ=PD可得:∠ADQ=30°,即Q的路径是一条线段,且线段DQ位于AD上方,易求得DQ=8
<PD≤8;②由∠QPD=120°,PQ=PD可得:∠ADQ=30°,即Q的路径是一条线段,且线段DQ位于AD上方,易求得DQ=8![]() ,BQ的最短距离即点B到DQ的垂线段长度,可求得span>DQ的最小值=3
,BQ的最短距离即点B到DQ的垂线段长度,可求得span>DQ的最小值=3![]() +4;
+4;
解:(1)如图1,连接PC,QP,PC交⊙P于T,
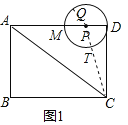
∵矩形ABCD
∴∠ADC=90°,CD=AB=6,AD=BC=8,
在Rt△CDP中,由勾股定理得:PC=![]() =
=![]() =4
=4![]() ,
,
∵∠QPD=120°,PD=2![]()
∴S扇形QPD=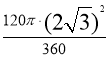 =4π
=4π
CT=CP-PT=4![]() -2
-2![]() =2
=2![]()
故答案为:4![]() ,4π,2
,4π,2![]() ;
;
(2)![]() 与
与![]() 相切时,设切点为点
相切时,设切点为点![]() ,
,
连接![]() ,则
,则![]() ,
,
![]() 四边形
四边形![]() 为矩形
为矩形
![]()
在![]() 中,
中,![]() ,
,![]() ,
,
![]()
在![]() 中,
中,![]()
设![]() 半径为
半径为![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]()
(3)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,
,
则![]()
又![]()
![]()
![]()
设![]() 半径为
半径为![]() ,则
,则![]() ,
,![]() ,
,
![]()
![]()
在![]() 中,
中,![]() ,
,![]()
![]()
在![]() 中,根据勾股定理得:
中,根据勾股定理得:![]()
解得:![]() (舍去),
(舍去),![]()
![]() 的长为4.
的长为4.
(4)①![]() ,或
,或![]()
②![]() ,
,![]()


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪个人先下棋,规则如下:三人手中各持有一枚质地均匀的硬币,他们同时将手中硬币抛落到水平地面为一个回合,落地后,三枚硬币中,恰有两枚正面向上或者反面向上的两人先下棋;若三枚硬币均为正面向上或反面向上,则不能确定其中两人先下棋.
(1)请你完成下面表示游戏一个回合所有可能出现的结果的树状图;
(2)求出一个回合能确定两人下棋的概率.
解:(1)树状图为:
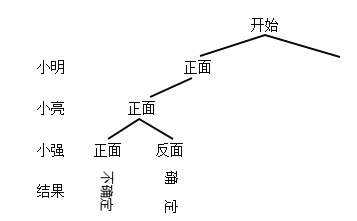
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.
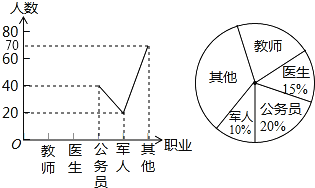
(1)把折线统计图补充完整;
(2)求出扇形统计图中,公务员部分对应的圆心角的度数;
(3)若从被调查的学生中任意抽取一名,求取出的这名学生最喜欢的职业是“教师”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的边
的边![]() 的垂直平分线,垂足为点
的垂直平分线,垂足为点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则下列结论:
,则下列结论:
①四边形![]() 是菱形;
是菱形;
②![]() ;
;
③![]() ;
;
④![]() 四边形
四边形![]()
以上四个结论中所有正确的结论是( )

A.①②B.①②③C.②④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示.
(分钟)之间的函数关系如图所示.
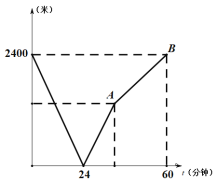
(1)根据图象信息,![]() 分钟时甲乙两人相遇,甲的速度为 米/分钟;
分钟时甲乙两人相遇,甲的速度为 米/分钟;
(2)求出线段![]() 所表示的函数表达式;
所表示的函数表达式;
(3)当甲,乙相距1000米时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、
丁四个班级植树情况进行了调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
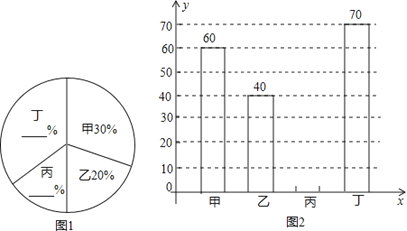
(1)这四个班共植树 棵;
(2)请你在答题卡上补全两幅统计图;
(3)求图1中“甲”班级所对应的扇形圆心角的度数;
(4)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树有多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
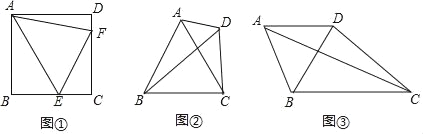
(1)如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,则线段BE、EF、FD之间的数量关系为 ;
(2)如图②,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边△ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;
问题解决
(3)如图③,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.
,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与
的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与![]() 交于点F,延长BA到点G,使得
交于点F,延长BA到点G,使得![]() ,连接FG.
,连接FG.
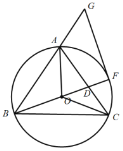

备用图
(1)求证:FG是![]() 的切线;
的切线;
(2)若![]() 的半径为4.
的半径为4.
①当![]() ,求AD的长度;
,求AD的长度;
②当![]() 是直角三角形时,求
是直角三角形时,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com