
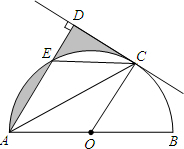
 如图,AB是⊙O直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连CE.
如图,AB是⊙O直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连CE.分析 (1)由OA=OC得∠OCA=∠OAC,由AC平分∠DAB得∠DAC=∠OAC,则∠ADC=∠OCA,根据平行线的判定得OC∥AD,由于AD⊥CD,根据平行线的性质得到OC⊥CD,然后根据切线的判定定理即可得到CD是⊙O的切线;
(2)由菱形的性质得到CE=OC=OE=1,△OCE都为等边三角形,得到∠COE=∠OCE=60°,易得∠DCE=30°,在Rt△DCE中,根据含30度的直角三角形三边的关系得DE、DC,所以易求S△DCE,由于弓形AE的面积=弓形CE的面积,所以S阴影=S△DCE.
解答 (1)证明:∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠ADC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结OE,如图,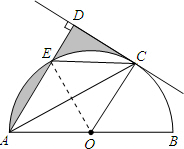
∵四边形OAEC为菱形,
∴CE=OC=OE=2,
∴△OCE都为等边三角形,
∴∠COE=∠OCE=60°,
而∠DCO=90°,
∴∠DCE=30°,
在Rt△DCE中,CE=1,
∴DE=$\frac{1}{2}$CE=$\frac{1}{2}$,DC=$\frac{\sqrt{3}}{2}$CE=$\frac{\sqrt{3}}{2}$,
∴S△DCE=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{8}$,
∵AE弧=CE弧,
∴弓形AE的面积=弓形CE的面积,
∴S阴影=S△DCE=$\frac{\sqrt{3}}{8}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了扇形的面积公式.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:选择题
| A. | a+2b | B. | b+2a | C. | 4a+6b | D. | 6a+4b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
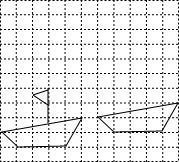 (1)如图,网格内每个小正方形的边长为1,小船从左边移到右边新的位置,试分析小船是怎样移到新的位置的,并将小船运动中缺少的部分补上.
(1)如图,网格内每个小正方形的边长为1,小船从左边移到右边新的位置,试分析小船是怎样移到新的位置的,并将小船运动中缺少的部分补上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
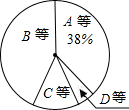 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | ||
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | ||
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com