
【题目】某市A,B两镇相距42千米,分别从A,B处测得某风景区中心C处的方位角如图所示,风景区区域是以C为圆心,15千米为半径的圆,tanα=1.673,tanβ=1.327.为了开发旅游,有关部门要设计修建连接A,B两市的县级公路.问连接A,B的两镇的县级公路是否穿过风景区,请说明理由.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=a.
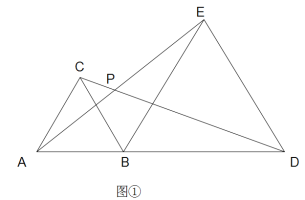
(1)当a=60°, 如图①则,∠DPE的度数______________
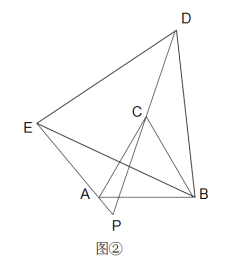
(2)若△BDE绕点B旋转一定角度,如图②所示,求∠DPE(用a表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在直线MN上求作一点P,使点P到射线OA和OB的距离相等.(要求用尺规作图,保留作图痕迹,不必写作法和证明过程)

(2)等腰三角形的两边长满足|a-4|+(b-9)2=0.求这个等腰三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠BAD=60°.动点E、F分别从点B、D同时出发,以1cm/s的速度向点A、C运动,连接AF、CE,取AF、CE的中点G、H,连接GE、FH.设运动的时间为ts(0<t<4).
(1)求证:AF∥CE;
(2)当t为何值时,四边形EHFG为菱形;
(3)试探究:是否存在某个时刻t,使四边形EHFG为矩形,若存在,求出t的值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限且OC=5,点B在x轴的正半轴上且OB=6,∠OAB=90°且OA=AB.
(1)求点A和点B的坐标;
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA成边AB于点Q,交边OC或边CB于点R,设点P的横坐标为t,线段QR的长度为m,已知t=4时,直线l恰好过点C,当0<t<3时,求m关于t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:
如图,△ABC的顶点都在方格纸的格点上,将△ABC向下平移2倍,再向右平移3格.
(1)请在图中画出平移后的△A′B′C′;
(2)在图中画出△的A′B′C′的高C′D′(标出点D′的位置);
(3)如果每个小正方形边长为1,则△A′B′C′的面积= .(答案直接填在题中横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.
(1)此时梯子顶端离地面多少米?
(2)若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com