
【题目】如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.
(1)判断直线BE与线段AD之间的关系,并说明理由;
(2)若∠C=30°,图中是否存在等边三角形?若存在,请写出来并证明;若不存在,请说明理由.

【答案】(1)BE垂直平分AD,理由见解析;(2)存在,△ABD、△GAE是等边三角形.
【解析】
(1)根据余角的性质即可得到∠5=∠C;由AD平分∠MAC,得到∠3=∠4,根据三角形的外角的性质得到∠BAD=∠ADB,推出△BAD是等腰三角形,于是得到结论.
(2)根据∠5=∠C=30°,AM⊥BC,可得∠ABD=60°,∠CAM=60°,进而得到∠ADB=∠4+∠C=60°,∠BAD=60°,依据∠ABD=∠BDA=∠BAD,可得△ABD是等边三角形;根据∠AEG=∠AGE=∠GAE,即可得到△AEG是等边三角形.
解:(1)BE垂直平分AD,理由:
∵AM⊥BC,
∴∠ABC+∠5=90°,
∵∠BAC=90°,
∴∠ABC+∠C=90°,
∴∠5=∠C;
∵AD平分∠MAC,
∴∠3=∠4,
∵∠BAD=∠5+∠3,∠ADB=∠C+∠4,∠5=∠C,
∴∠BAD=∠ADB,
∴△BAD是等腰三角形,
又∵∠1=∠2,
∴BE垂直平分AD;
(2)△ABD、△GAE是等边三角形.理由:
∵∠5=∠C=30°,AM⊥BC,
∴∠ABD=60°,
∵∠BAC=90°,
∴∠CAM=60°,
∵AD平分∠CAM,
∴∠4=![]() ∠CAM=30°,
∠CAM=30°,
∴∠ADB=∠4+∠C=60°,
∴∠BAD=60°,
∴∠ABD=∠BDA=∠BAD,
∴△ABD是等边三角形;
∵在Rt△BGM中,∠BGM=60°=∠AGE,
在Rt△ACM中,∠CAM=60°,
∴∠AEG=∠AGE=∠GAE,
∴△AEG是等边三角形.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点A到航线![]() 的距离为2km,点B位于点A北偏东60°方向且与A相距10km.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5分钟后该轮船行至点A的正北方向的D处.
的距离为2km,点B位于点A北偏东60°方向且与A相距10km.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5分钟后该轮船行至点A的正北方向的D处.
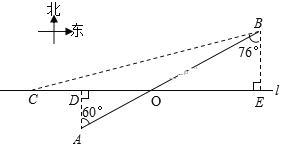
(1)求观测点B到航线![]() 的距离;
的距离;
(2)求该轮船航行的速度(结果精确到0.1km/h).
(参考数据: ![]() ≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=x2+bx-1的图象经过点(2,3).
(1)求这个函数的表达式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)观察图象,说明y随x的增大是怎样变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形 ABCD 中,放入六个形状大小相同的长方形,所标尺寸如图所示, 则图中阴影部分面积为( )

A. 44cm2B. 36cm2C. 96 cm2D. 84cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两人骑自行车绕800米圆形跑道行驶,他们从同一地点出发,如果方向相反,每一分二十秒相遇一次,如果方向相同,每十三分二十秒相遇一次.假设二人速度不等,求各人速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB = 90o,AC =6,BC = 8,点F在线段AB上,以点B为圆心,BF为半径的圆交BC于点E,射线AE交圆B于点D(点D、E不重合).
(1)如果设BF = x,EF = y,求y与x之间的函数关系式,并写出它的定义域;
(2)如果![]() ,求ED的长;
,求ED的长;
(3)联结CD、BD,请判断四边形ABDC是否为直角梯形?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com