
探究与发现:
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
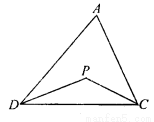
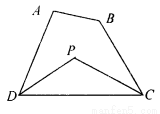
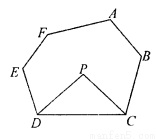
图1 图2 图3
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:__ __ __.
【解析】
试题分析:探究一:根据角平分线的定义可得∠PDC= ∠ADC,∠PCD=
∠ADC,∠PCD= ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究二:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究三:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.
试题解析:探究一:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC= ∠ADC,∠PCD=
∠ADC,∠PCD= ∠ACD,
∠ACD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°- ∠ADC-
∠ADC- ∠ACD,
∠ACD,
=180°- (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°- (180°-∠A),
(180°-∠A),
=90°+ ∠A;
∠A;
探究二:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC= ∠ADC,∠PCD=
∠ADC,∠PCD= ∠BCD,
∠BCD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°- ∠ADC-
∠ADC- ∠BCD,
∠BCD,
=180°- (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°- (360°-∠A-∠B),
(360°-∠A-∠B),
= (∠A+∠B);
(∠A+∠B);
探究三:六边形ABCDEF的内角和为:(6-2)•180°=720°,
∵DP、CP分别平分∠ADC和∠ACD,
∴∠P= ∠ADC,∠PCD=
∠ADC,∠PCD= ∠ACD,
∠ACD,
∴∠P=180°-∠PDC-∠PCD,
=180°- ∠ADC-
∠ADC- ∠ACD,
∠ACD,
=180°- (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°- (720°-∠A-∠B-∠E-∠F),
(720°-∠A-∠B-∠E-∠F),
= (∠A+∠B+∠E+∠F)-180°,
(∠A+∠B+∠E+∠F)-180°,
即∠P= (∠A+∠B+∠E+∠F)-180°.
(∠A+∠B+∠E+∠F)-180°.
考点: 1.多边形内角与外角;2.三角形内角和定理.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:2016届江苏省兴化市七年级下学期期中考试数学试卷(解析版) 题型:选择题
下列从左到右的变形属于因式分解的是()
A.x2–2xy+y2=x(x-2y)+y2 B.x2-16y2=(x+8y)(x-8y)
C.x2+xy+y2=(x+y)2 D.x4y4-1=(x2y2+1)(xy+1)(xy-1)
查看答案和解析>>
科目:初中数学 来源:2016届江苏泰兴楚水实验中学七年级下学期第一次调研数学卷(解析版) 题型:填空题
在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于______度.

查看答案和解析>>
科目:初中数学 来源:2016届江苏无锡市七年级下学期期中考试数学卷(解析版) 题型:解答题
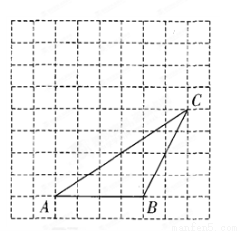
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源:2016届江苏扬州中学树人学校七年级上学期期末考试数学试卷(解析版) 题型:选择题
如下数表是由从1开始的连续自然数组成,则自然数2014所在的行数是

A.第45行 B.第46行 C.第47行 D.第48行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com