
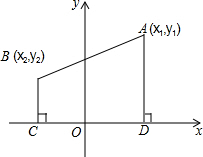
 如图,A(x1,y1),B (x2,y2)是直角坐标系中的任意两点,AD,BC都垂直于x轴,点D,C分别为垂足
如图,A(x1,y1),B (x2,y2)是直角坐标系中的任意两点,AD,BC都垂直于x轴,点D,C分别为垂足分析 (1)由于AD,BC都垂直于x轴,点D,C分别为垂足,则AD=|y1|,BC=|y2|,则|AD-BC|=|y1-y2|,CD直接用两点的横坐标之差的绝对值表示;
(2)利用勾股定理求解;
(3)把点(-1,3)和点(-5,7)直接代入(2)中的公式中计算即可.
解答  解:(1)|AD-BC|=|y1-y2|,CD=|x1-x2|;
解:(1)|AD-BC|=|y1-y2|,CD=|x1-x2|;
(2)AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$;
(3)点(-1,3)与点(-5,7)之间的距离=$\sqrt{(-1+5)^{2}+(3-7)^{2}}$=4$\sqrt{2}$.
点评 本题考查了两点间的距离公式:设有两点A(x1,y1),B(x2,y2),则这两点间的距离为AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$.求直角坐标系内任意两点间的距离可直接套用此公式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
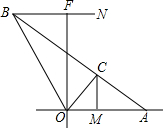 如图,一轮渡从B点出发沿东偏南25°方向匀速航行,经过4.5分钟后达到C处,若保持航线不变,继续航行可直接到达停靠码头A,在停靠码头A的正西反向500m处有一观察站O,在O处测得B位于其北偏西35°,C位于其北偏东55°.求C处到海岸线OA的距离大约是多少米?
如图,一轮渡从B点出发沿东偏南25°方向匀速航行,经过4.5分钟后达到C处,若保持航线不变,继续航行可直接到达停靠码头A,在停靠码头A的正西反向500m处有一观察站O,在O处测得B位于其北偏西35°,C位于其北偏东55°.求C处到海岸线OA的距离大约是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
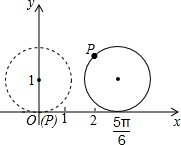 如图,在平面直角坐标系中,半径为1的圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动,当滚动到圆心位于($\frac{5π}{6}$,1)时,点P的坐标是($\frac{5π-3}{6}$,$\frac{2+\sqrt{3}}{2}$).
如图,在平面直角坐标系中,半径为1的圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动,当滚动到圆心位于($\frac{5π}{6}$,1)时,点P的坐标是($\frac{5π-3}{6}$,$\frac{2+\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知实数a、b、c在数轴上的位置如图所示,试化简:$\sqrt{{{(-c)}^2}}-|{a-c}|+\sqrt{{{(a+b)}^2}}-|{b+c}|$.
已知实数a、b、c在数轴上的位置如图所示,试化简:$\sqrt{{{(-c)}^2}}-|{a-c}|+\sqrt{{{(a+b)}^2}}-|{b+c}|$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一张边长为6$\sqrt{2}$cm的正方形纸板,现将该纸板的四个角剪掉,制作一个有底无盖的长方体盒子,剪掉的四个角是面积相等的小正方形,此小正方形的边长为$\sqrt{2}$cm.求:
如图,有一张边长为6$\sqrt{2}$cm的正方形纸板,现将该纸板的四个角剪掉,制作一个有底无盖的长方体盒子,剪掉的四个角是面积相等的小正方形,此小正方形的边长为$\sqrt{2}$cm.求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}xy=1\\ x-y=2\end{array}$ | B. | $\left\{\begin{array}{l}5x-2y=3\\ \frac{1}{x}-y=3\end{array}$ | C. | $\left\{\begin{array}{l}2x-z=0\\ 3x-y=\frac{1}{5}\end{array}$ | D. | $\left\{\begin{array}{l}x=5\\ \frac{x}{2}-\frac{y}{3}=7\end{array}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com