
【题目】如图,已知在△ABC中,点D,E,F分别在BC,AB,AC边上.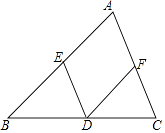
(1)当点D,E,F分别为BC,AB,AC边的中点时,求证:△BED≌△DFC;
(2)若DE∥AC,DF∥AB,且AE=2,BE=3,求 ![]() 的值.
的值.
【答案】
(1)证明:∵点D,E,F分别为BC,AB,AC边的中点,
∴DE和DF为△ABC的中位线,
∴DE∥AC,DF∥AB,
∴∠BDE=∠C,∠B=∠CDF,
∴△BED≌△DFC
(2)解:DE∥AC,DF∥AB,
∴∠BDE=∠C,∠B=∠CDF,四边形AEDF为平行四边形,
∴△BED∽△DFC,DF=AE=2,DE=AF,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
【解析】(1)依据三角形的中位线定理可得到DE∥AC,DF∥AB,然后依据平行线的性质可证明∠BDE=∠C,∠B=∠CDF,最后,再依据SAS证明△BED≌△DFC即可;
(2)首先证明△BED∽△DFC,然后依据相似三角形的性质求解即可.
【考点精析】掌握平行线分线段成比例是解答本题的根本,需要知道三条平行线截两条直线,所得的对应线段成比例.


科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有8个红球,4个黄球,3个白球,他们除了颜色外都相同,两人做游戏,游戏规则如下:一个人抓住袋子,一个人摸球,若摸出红球,摸球者胜,否则拿袋子的人获胜.
(1)如果你参加游戏,为了尽可能的获胜,你是做摸球的人还是做拿袋子的人?为什么?
(2)你说这个游戏公平吗?如果公平,说明理由:如果不公平,请给出修改建议,使它对双方都是公平的.
查看答案和解析>>
科目:初中数学 来源: 题型:
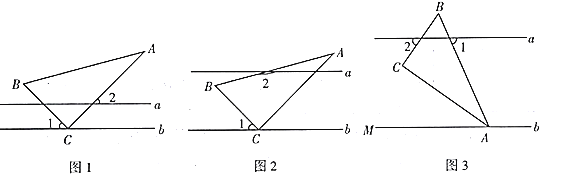
【题目】在综合与实践课上,同学们以“一个含![]() 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线![]() 且
且![]() 和直角三角形
和直角三角形![]() ,
,![]() ,
,![]() ,
,![]() .
.
操作发现:
(1)在如图1中,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,创新小组的同学把直线![]() 向上平移,并把
向上平移,并把![]() 的位置改变,发现
的位置改变,发现![]() ,说明理由;
,说明理由;
实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,![]() 平分
平分![]() ,此时发现
,此时发现![]() 与
与![]() 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() 的图象经过点A(1,3).
的图象经过点A(1,3).
(1)试确定此反比例函数的解析式;
(2)当x=2时,求y的值;
(3)当自变量x从5增大到8时,函数值y是怎样变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离![]() 米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )

A. 2米B. 2.5米C. 2.25米D. 3米
查看答案和解析>>
科目:初中数学 来源: 题型:
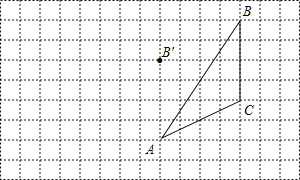
【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)补全△A′B′C′根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
(1)原理:对于任意两个实数a、b,
若ab>0,则a和b同号,即:![]() 或
或![]() ;
;
若ab<0,则a和b异号,即:![]() 或
或![]() ;
;
(2)对不等式(x+1)(x﹣2)>0来说,把(x+1)和(x﹣2)看成两个数a和b,所以按照上述原理可知:(Ⅰ)![]() 或(Ⅱ)
或(Ⅱ)![]() ,所以不等式(x+1)(x﹣2)>0的求解就转化求解不等式组(I)和(Ⅱ).
,所以不等式(x+1)(x﹣2)>0的求解就转化求解不等式组(I)和(Ⅱ).
(3)应用:解不等式x2﹣x﹣12>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )

A. 6 B. 12 C. 16 D. 20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com