
 如图,OA=OB,OC=OD,∠AOC=∠BOD,求证:AB∥CD.
如图,OA=OB,OC=OD,∠AOC=∠BOD,求证:AB∥CD.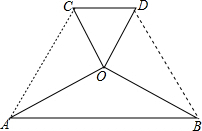 证明:连接AC、BD,
证明:连接AC、BD,
|


科目:初中数学 来源: 题型:
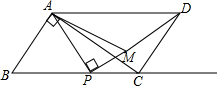 已知:平行四边形ABCD中,对角线AC⊥AB,AB=15,AC=20,点P为射线BC上一动点,AP⊥PM(点M与点B分别在直线AP的两侧),且∠PAM=∠CAD,连接MD.
已知:平行四边形ABCD中,对角线AC⊥AB,AB=15,AC=20,点P为射线BC上一动点,AP⊥PM(点M与点B分别在直线AP的两侧),且∠PAM=∠CAD,连接MD.查看答案和解析>>
科目:初中数学 来源: 题型:
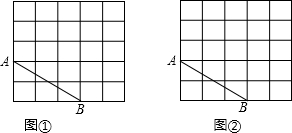 如图,在每个小正方形的边长均为1的方格纸中有一条线段AB,线段AB的两个端点均在小正方形的顶点上,请在图①、图②中各画一个三角形,它们的顶点均在小正方形的顶点上,且满足以下要求:
如图,在每个小正方形的边长均为1的方格纸中有一条线段AB,线段AB的两个端点均在小正方形的顶点上,请在图①、图②中各画一个三角形,它们的顶点均在小正方形的顶点上,且满足以下要求:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 某校各选拔了5名同学参加学校举行的“安全知识”比赛活动,比赛结果如图.
某校各选拔了5名同学参加学校举行的“安全知识”比赛活动,比赛结果如图.| 班级 | 平均数(分) | 中位数(分) | 众数 |
| 八(1) | 85 | ||
| 八(2) | 80 | 80 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
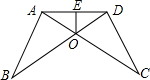 如图,AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE
如图,AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com