
| A. | 3组 | B. | 4组 | C. | 5组 | D. | 6组 |
分析 根据平行四边形的判定方法分别判断得出即可.
解答 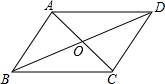 解:①根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,可知①能判定这个四边形是平行四边形;
解:①根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,可知①能判定这个四边形是平行四边形;
②根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,可知②能判定这个四边形是平行四边形;
③根据平行四边形的判定定理:两条对角线互相平分的四边形是平行四边形,可知③能判定这个四边形是平行四边形;
④根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,可知④不能判定这个四边形是平行四边形;
⑤根据平行四边形的判定定理:两组对角分别相等的四边形是平行四边形,可知⑤能判定这个四边形是平行四边形;
⑥∵∠A+∠B=180°,∠A+∠D=180°,
∴AD∥BC,AB∥CD,
根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,可知⑥能判定这个四边形是平行四边形;
∴一定能判定这个四边形是平行四边形的条件共有5组,
故选:C.
点评 此题主要考查了平行四边形的判定方法;准确无误的掌握平行四边形的判定方法是解题关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
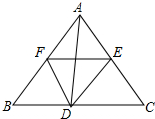 在△ABC中,D,E,F分别是BC、AB、AC的中点.
在△ABC中,D,E,F分别是BC、AB、AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知一艘渔船上的渔民在B处看见灯塔M在北偏东27°方向,这艘渔船以28海里/时的速度向正西方向航行,半小时后到达A处,在A处看见灯塔M在北偏东60°方向,请你运用以上测得的数据求出此时灯塔M与渔船的距离.
如图,已知一艘渔船上的渔民在B处看见灯塔M在北偏东27°方向,这艘渔船以28海里/时的速度向正西方向航行,半小时后到达A处,在A处看见灯塔M在北偏东60°方向,请你运用以上测得的数据求出此时灯塔M与渔船的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
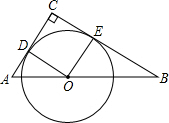 如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.
如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
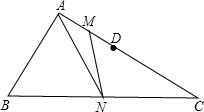 如图,在△ABC中,∠BAC=90°,点D在边AC上,AB=CD,点M、N分别为AD、BC的中点,连接MN、AN,MN=3$\sqrt{2}$,AD=4,则线段AN的长为$\sqrt{34}$.
如图,在△ABC中,∠BAC=90°,点D在边AC上,AB=CD,点M、N分别为AD、BC的中点,连接MN、AN,MN=3$\sqrt{2}$,AD=4,则线段AN的长为$\sqrt{34}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com