
【题目】在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,且BF∥CD,AF⊥CE的延长线于F.连接DE交对角线AC于H.下列结论:①△ACD≌ACE;②AC垂直平分ED;③CE=2BF;④CE平分∠ACB.其中结论正确的是________.(填序号)

【答案】①②③④
【解析】
由已知条件可直接证得△ACD≌△ACE;由三角形全等的性质可得CD=CE,又因为AD=AE所以AC是DE的垂直平分线即AC垂直平分ED;延长AF,CB相交于点G,证出△ABG≌△CBE,则AG=CE=CD,再证出AG=2BF即可得出③正确;取CE的中点I连接BI,可得CE=2BI,再证明BF=BI,再利用三角形的外角性质和平行线的性质问题④可得证.
解:①∵AD∥BC,∠ABC=90°,
∴∠BAD=90°.
∵AB=CB,
∴∠BAC=45°,
∴∠DAC=45°.
又∵AC=AC,AE=AD,
∴△AEC≌△ADC.
故①正确.
②∵△AEC≌△ADC,
∴DC=CE.
又∵AD=AE,
∴AC是DE的垂直平分线.
即AC垂直平分ED.
故②正确.
③延长AF,CB相交于点G,则∠ABG=∠ABC=90°,

∵∠BEC+∠BCE=90°,
又∵AF⊥CE,
∴∠AEF+∠BAG=90°,
∵∠BEC=∠AEF,
∴∠BCE=∠BAG,
又∵AB=BC,
∴△ABG≌△CBE,
∴AG=CE=CD,
又∵AD//BC,
∴∠G=∠DCG,
∵BF//CD,
∴∠DCG=∠FBG,
∴∠G=∠FBG,
∴BF=FG.
又∵∠ABG=90°,
∴AG=2BF.
即CE=2BF.
故③正确;
④取CE的中点I,连接BI,则BI=CI=EI.

∴∠CBI=∠BCI,
∴∠BIF=2∠BCI.
∵CE=2BF,
∴BF=BI,
∴∠BFI=∠BIF=2∠BCI.
∵BF//CD,
∴∠BFI=∠DCE,
∴∠BCI=![]() ∠DCE=∠ACE,
∠DCE=∠ACE,
∴CE平分∠ACB.
故④正确.
故答案为:①②③④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里有4个标有1,2,3,4的小球,它们的形状、大小完全相同.小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜,若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AC=10,S△ABC =25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是( )

A. 4 B. ![]() C. 5 D. 6
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RT△ABC中,∠ACB=90°,∠B=35°,CD⊥AB,垂足为点D,

(1)求∠ACD的度数;
(2)找出图中相等的角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技馆是少年儿童节假日游玩的乐园.
如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y=![]() ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=a.
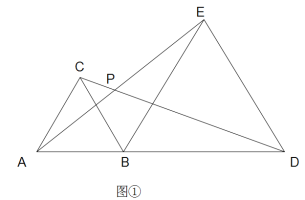
(1)当a=60°, 如图①则,∠DPE的度数______________
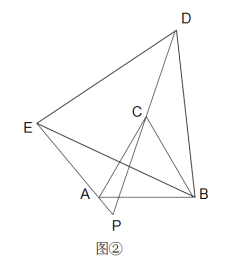
(2)若△BDE绕点B旋转一定角度,如图②所示,求∠DPE(用a表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com