
ЎѕМвДїЎїГїДкПДјѕИ«№ъёчµШЧЬУРОґіЙДкИЛТтДзЛ®¶шЙҐК§ЙъГьЈ¬БоИЛНґРДјІКЧЈ®ЅсДкДіРЈОЄИ·±ЈС§Йъ°ІИ«Ј¬їЄХ№БЛЎ°Ф¶АлДзЛ®Ў¤Хд°®ЙъГьЎ±µД·АДзЛ®°ІИ«ЦЄК¶ѕєИьЈ®ПЦґУёГРЈЖЯЎў°ЛДкј¶ЦРёчЛж»ъійИЎ10ГыС§ЙъµДѕєИьіЙјЁЈЁ°Щ·ЦЦЖЈ©ЅшРРХыАнЎўГиКцєН·ЦОцЈЁіЙјЁµГ·ЦУГx±нКѕЈ¬№І·ЦіЙЛДЧйЈєAЈ®80ЎЬxЎЬ85Ј¬BЈ®85ЎЬxЎЬ90Ј¬CЈ®90ЎЬxЎЬ95Ј¬DЈ®95ЎЬxЎЬ100Ј©Ј¬ПВГжёшіцБЛІї·ЦРЕПўЈє
ЖЯДкј¶10ГыС§ЙъµДѕєИьіЙјЁКЗЈє99Ј¬80Ј¬99Ј¬86Ј¬99Ј¬96Ј¬96Ј¬100Ј¬89Ј¬82
°ЛДкј¶10ГыС§ЙъµДѕєИьіЙјЁФЪCЧйЦРµДКэѕЭКЗ:94Ј¬90Ј¬94
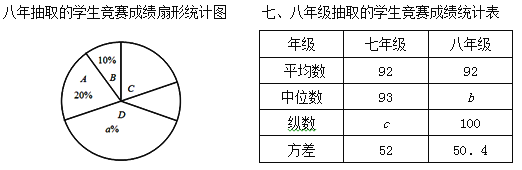
ёщѕЭТФЙПРЕПўЈ¬ЅвґрПВБРОКМвЈє
ЈЁ1Ј©Ц±ЅУРґіцЙПКцНј±нЦРaЈ¬bЈ¬cµДЦµЈ»
ЈЁ2Ј©ёщѕЭТФЙПКэѕЭЈ¬ДгИПОЄёГРЈЖЯЎў°ЛДкј¶ЦРДДёцДкј¶С§ЙъХЖОХ·АДзЛ®°ІИ«ЦЄК¶ЅПєГЈїЗлЛµГчАнУЙЈЁТ»МхАнУЙјґїЙЈ©Ј»
ЈЁ3Ј©ёГРЈЖЯЎў°ЛДкј¶№І730ИЛІОјУБЛґЛґОѕєИь»о¶ЇЈ¬№АјЖІОјУґЛґОѕєИь»о¶ЇіЙјЁУЕРгЈЁxЁR90Ј©µДС§ЙъИЛКэКЗ¶аЙЩЈї
Ўѕґр°ёЎїЈЁ1Ј©a=40Ј¬b=94Ј¬c=99Ј»ЈЁ2Ј©°ЛДкј¶Ј¬јыЅвОцЈ»ЈЁ3Ј©ІОјУґЛґОѕєИь»о¶ЇіЙјЁУЕРгµДИЛКэКЗ468ИЛ.
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭЦРО»КэєНЦЪКэµД¶ЁТејґїЙµГµЅЅбВЫЈ»ЈЁ2Ј©ёщѕЭ°ЛДкј¶µДЦРО»КэєНЦЪКэѕщёЯУЪЖЯДкј¶УЪКЗµГµЅ°ЛДкј¶С§ЙъХЖОХ·АДзЛ®°ІИ«ЦЄК¶ЅПєГЈ»ЈЁ3Ј©АыУГСщ±ѕ№АјЖЧЬМеЛјПлЗуЅвїЙµГ.
ЅвЈєЈЁ1Ј©![]() Ј¬
Ј¬
ЎЯ°ЛДкј¶10ГыС§ЙъµДѕ№ИьіЙјЁµДЦРО»КэКЗµЪ5єНµЪ6ёцКэѕЭµДЖЅ·ЅКэЈ¬
Ўа ![]()
ЎЯФЪЖЯДкј¶10ГыС§ЙъµДѕ№ИьіЙјЁЦР99іцПЦµДґОКэЧо¶аЈ¬
Ўаc=99Ј»
ЈЁ2Ј©°ЛДкј¶С§ЙъХЖОХ·АДзЛ®°ІИ«ЦЄК¶ЅПєГЈ¬АнУЙЈєЛдИ»ЖЯЎў°ЛДкј¶µДЖЅѕщ·ЦѕщОЄ92·ЦЈ¬µ«°ЛДкј¶µДЦРО»КэєНЦЪКэѕщёЯУЪЖЯДкј¶.
ЈЁ3Ј©ІОјУґЛґОѕєИь»о¶ЇіЙјЁУЕРгЈЁxЎЭ90Ј©µДС§ЙъИЛКэ=720ЎБ![]() =468ИЛЈ¬
=468ИЛЈ¬
ґрЈєІОјУґЛґОѕєИь»о¶ЇіЙјЁУЕРгЈЁxЎЭ90Ј©µДС§ЙъИЛКэКЗ468ИЛ.



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї јЧЎўТТБЅГыН¬С§ІОјУЙЩДкїЖјјґґРВСЎ°ОИьЈ¬БщґО±ИИьµДіЙјЁИзПВЈє
јЧЈє87 93 88 93 89 90
ТТЈє85 90 90 96 89 a
ЈЁ1Ј©јЧН¬С§іЙјЁµДЦРО»КэКЗЎЎ ЎЎЈ»
ЈЁ2Ј©ИфјЧЎўТТµДЖЅѕщіЙјЁПаН¬Ј¬ФтaЈЅЎЎ ЎЎЈ»
ЈЁ3Ј©ТСЦЄТТµД·ЅІоКЗ![]() Ј¬Из№ыТЄСЎЕЙТ»Гы·ў»УОИ¶ЁµДН¬С§ІОјУ±ИИьЈ¬У¦ёГСЎЛЈїЛµГчАнУЙЈ®ЈЁ·ЅІо№«КЅЈєS2ЈЅ
Ј¬Из№ыТЄСЎЕЙТ»Гы·ў»УОИ¶ЁµДН¬С§ІОјУ±ИИьЈ¬У¦ёГСЎЛЈїЛµГчАнУЙЈ®ЈЁ·ЅІо№«КЅЈєS2ЈЅ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЛДО»Н¬С§ФЪСРѕїєЇКэyЈЅax2+bx+c(aЎўbЎўcОЄіЈКэЈ¬ЗТaЎЩ0)К±Ј¬јЧ·ўПЦµ±xЈЅ1К±Ј¬єЇКэУРЧоґуЦµЈ»ТТ·ўПЦ©Ѓ1КЗ·ЅіМax2+bx+cЈЅ0µДТ»ёцёщЈ»±ы·ўПЦєЇКэµДЧоґуЦµОЄ©Ѓ1Ј»¶Ў·ўПЦµ±xЈЅ2К±Ј¬yЈЅ©Ѓ2Ј¬ТСЦЄЛДО»ЦРЦ»УРТ»О»·ўПЦµДЅбВЫК±ґнОуµДЈ¬ФтёГН¬С§КЗ( ).
A. јЧB. ТТC. ±ыD. ¶Ў
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪТ»Мх±КЦ±µД¶«ОчПтєЈ°¶ПЯlЙПУРТ»і¤ОЄ1.5kmµДВлН·MNєНµЖЛюCЈ¬µЖЛюCѕаВлН·µД¶«¶ЛNУР20km.Т»ВЦґ¬ТФ36km/hµДЛЩ¶ИєЅРРЈ¬ЙПОз10Јє00ФЪAґ¦ІвµГµЖЛюCО»УЪВЦґ¬µД±±Ж«Оч30Ўг·ЅПтЈ¬ЙПОз10Јє40ФЪBґ¦ІвµГµЖЛюCО»УЪВЦґ¬µД±±Ж«¶«60Ўг·ЅПтЈ¬ЗТУлµЖЛюCПаѕа12km.
(1)ИфВЦґ¬ХХґЛЛЩ¶ИУлєЅПтєЅПтЈ¬єОК±µЅґпєЈ°¶ПЯЈї
(2)ИфВЦґ¬І»ёД±дєЅПтЈ¬ёГВЦґ¬ДЬ·сНЈїїФЪВлН·ЈїЗлЛµГчАнУЙ(ІОїјКэѕЭЈє ![]() ЎЦ1.4Ј¬
ЎЦ1.4Ј¬ ![]() ЎЦ1.7)Ј®
ЎЦ1.7)Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј1Ј¬ФЪABCDЦРЈ¬AEЎНBCУЪEЈ¬EЗЎОЄBCµДЦРµгЈ®tanBЈЅ2Ј®
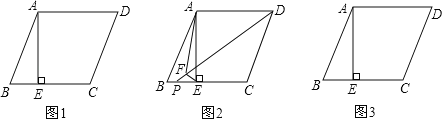
ЈЁ1Ј©ЗуЦ¤ЈєADЈЅAEЈ»
ЈЁ2Ј©ИзНј2Ј®µгPФЪBEЙПЈ¬ЧчEFЎНDPУЪµгFЈ¬Б¬ЅбAFЈ®ПЯ¶ОDFЎўEFУлAFЦ®јдУРФхСщµДКэБї№ШПµЈїІўЛµГчАнУЙЈ»
ЈЁ3Ј©ЗлДгФЪНј3ЦР»НјМЅѕїЈєµ±PОЄЙдПЯECЈ¬ЙПИОТвТ»µгЈЁPІ»УлµгEЦШєПЈ©К±Ј¬ЧчEFЎНDPУЪµгFЈ¬Б¬ЅбAFЈ¬ПЯ¶ОDFЎўEFУлAFЦ®јдУРФхСщµДКэБї№ШПµЈїЗлФЪНј3ЦРІ№И«НјРОЈ¬Ц±ЅУРґіцЅбВЫЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ЎчABCµД¶ҐµгЧш±к·Ц±рОЄAЈЁ©Ѓ1Ј¬1Ј©Ј¬BЈЁ0Ј¬©Ѓ2Ј©Ј¬CЈЁ1Ј¬0Ј©Ј¬µгPЈЁ0Ј¬2Ј©ИЖµгAРэЧЄ180ЎгµГµЅµгP1Ј¬µгP1ИЖµгBРэЧЄ180ЎгµГµЅµгP2Ј¬µгP2ИЖµгCРэЧЄ180ЎгµГµЅµгP3Ј¬µгP3ИЖµгAРэЧЄ180ЎгµГµЅµгP4Ј¬ЎЈ¬°ґґЛЧч·ЁЅшРРПВИҐЈ¬ФтµгP2019µДЧш±кОЄЈЁ Ј©
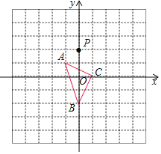
A.ЈЁ-2Ј¬0Ј©B.![]() C.ЈЁ2Ј¬-4Ј©D.ЈЁ-2Ј¬-2Ј©
C.ЈЁ2Ј¬-4Ј©D.ЈЁ-2Ј¬-2Ј©
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Хэ·ЅРОABCDµД±Яі¤ОЄ3cmЈ¬¶ЇµгMґУµгBіц·ўТФ3cm/sµДЛЩ¶ИСШЧЕ±ЯBC©ЃCD©ЃDAФЛ¶ЇЈ¬µЅґпµгAНЈЦ№ФЛ¶ЇЈ¬БнТ»¶ЇµгNН¬К±ґУµгBіц·ўЈ¬ТФ1cm/sµДЛЩ¶ИСШЧЕ±ЯBAПтµгAФЛ¶ЇЈ¬µЅґпµгAНЈЦ№ФЛ¶ЇЈ¬ЙиµгMФЛ¶ЇК±јдОЄxЈЁsЈ©Ј¬ЎчAMNµДГж»эОЄyЈЁcm2Ј©Ј¬Фтy№ШУЪxµДєЇКэНјПуКЗЈЁЎЎЎЎЈ©

A.  B.
B. 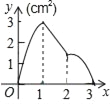 C.
C.  D.
D. 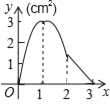
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
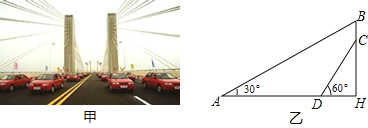
ЎѕМвДїЎїДіґуЗЕІЙУГµНЛюР±АЗЕЗЕРНЈЁИзјЧНјЈ©Ј¬НјТТКЗґУНјјЧТэЙкіцµДЖЅГжНјЈ¬јЩЙиДгХѕФЪЗЕЙПІвµГАЛчABУлЛ®ЖЅЗЕГжµДјРЅЗКЗ30ЎгЈ¬АЛчCDУлЛ®ЖЅЗЕГжµДјРЅЗКЗ60ЎгЈ¬БЅАЛч¶Ґ¶ЛµДѕаАлBCОЄ2ГЧЈ¬БЅАЛчµЧ¶ЛѕаАлADОЄ20ГЧЈ¬ЗлЗуіцБўЦщBHµДі¤Ј®ЈЁЅб№ыѕ«И·µЅ0.1ГЧЈ¬ ![]() ЎЦ1.73Ј©
ЎЦ1.73Ј©
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЅсДкЎ°ОеТ»Ў±јЩЖЪЈ¬ДіКэС§»о¶ЇРЎЧйЧйЦЇТ»ґОµЗЙЅ»о¶Ї.ЛыГЗґУЙЅЅЕПВAµгіц·ўСШР±ЖВABµЅґпBµгЈ¬ФЩґУBµгСШР±ЖВBCµЅґпЙЅ¶ҐCµгЈ¬В·ПЯИзНјЛщКѕ.Р±ЖВABµДі¤ОЄ1000ГЧЈ¬Р±ЖВBCµДі¤ОЄ200![]() ГЧЈ¬ФЪCµгІвµГBµгµДё©ЅЗОЄ45ЎгЈ¬ТСЦЄAµгєЈ°О21ГЧЈ¬CµгєЈ°О721ГЧ.
ГЧЈ¬ФЪCµгІвµГBµгµДё©ЅЗОЄ45ЎгЈ¬ТСЦЄAµгєЈ°О21ГЧЈ¬CµгєЈ°О721ГЧ.
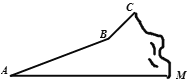
(1)ЗуBµгµДєЈ°ОЈ»
(2)ЗуР±ЖВABµДЖВЅЗ.
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com