

分析 (1)在平面直角坐标系中可以直接找出答案;
(2)根据求出的各点坐标,得出规律;
(3)点A100中的n正好是4的倍数,根据第二问的答案可以分别得出点A100和A101的坐标,所以可以得到蚂蚁从点A100到A101的移动方向.
解答 解:(1)A1(0,1),A3(1,0),A12(6,0);
(2)当n=1时,A4(2,0),
当n=2时,A8(4,0),
当n=3时,A12(6,0),
所以A4n(2n,0);
(3)点A100中的n正好是4的倍数,所以点A100和A101的坐标分别是A100(50,0),A101的(50,1),所以蚂蚁从点A100到A101的移动方向是从下向上.
点评 本题主要考查的是在平面直角坐标系中确定点的坐标和点的坐标的规律性.运用由特殊到一般的数学思想方法得到一般规律是解决问题的关键.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
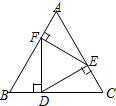 如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )
如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )| A. | 1:3 | B. | 2:3 | C. | $\sqrt{3}$:2 | D. | $\sqrt{3}$:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
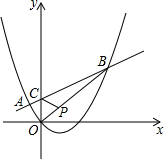 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}{x^2}-\frac{1}{2}$x与直线y=$\frac{1}{2}x+\frac{3}{2}$交于A、B,直线AB交于y轴于点C,点P为线段OB上一个动点(不与点O、B重合),当△OPC为等腰三角形时,点P的坐标:P1($\frac{3\sqrt{2}}{4}$,$\frac{3\sqrt{2}}{4}$),P2($\frac{3}{4}$,$\frac{3}{4}$),P3($\frac{3}{2}$,$\frac{3}{2}$).
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}{x^2}-\frac{1}{2}$x与直线y=$\frac{1}{2}x+\frac{3}{2}$交于A、B,直线AB交于y轴于点C,点P为线段OB上一个动点(不与点O、B重合),当△OPC为等腰三角形时,点P的坐标:P1($\frac{3\sqrt{2}}{4}$,$\frac{3\sqrt{2}}{4}$),P2($\frac{3}{4}$,$\frac{3}{4}$),P3($\frac{3}{2}$,$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com