
分析 (1)过△ABC的内心作直线即可.
(2)小华不会成功.直线CD可能平分△ABC的面积,若也平分周长,则AC=BC,与题中的AC≠BC冲突,故不会成功;
(3)①若直线经过顶点,则AC边上的中垂线即为所求.②若直线不过顶点,可分以下三种情况考虑:(a)直线与BC、AC分别交于E、F,CF=5,CE=3;(b)直线与AB、AC分别交于M、N,AM=3,AN=5,(c)直线与AB、BC分别交于P、Q,此种情况不存在.则符合条件的直线共有三条.
解答 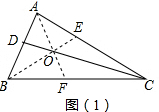 解:(1)如图(1)所示,分别作∠BAC与∠ABC的平分线AF,BE,两线交于点O,作直线CO交AB于D,直线CD即为所求;
解:(1)如图(1)所示,分别作∠BAC与∠ABC的平分线AF,BE,两线交于点O,作直线CO交AB于D,直线CD即为所求;
(2)小华不会成功.
如图(2),若直线CD平分△ABC的面积,过C作CE⊥AB于E,
那么S△ADC=S△DBC,
∴$\frac{1}{2}$AD•CE=$\frac{1}{2}$BD•CE,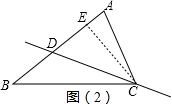
∴BD=AD,
∵AC≠BC,
∴AD+AC≠BD+BC,
∴小华不会成功;
(3)①若直线经过顶点,则AC边上的中垂线即为所求.
②若直线不过顶点,可分以下三种情况: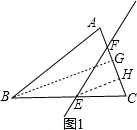
(a)直线与BC、AC分别交于E、F,如图1所示,
过点E作EH⊥AC于点H,过点B作BG⊥AC于点G,
易求,BG=4,AG=CG=3,
设CF=x,则CE=8-x,
由△CEH∽△CBG,可得EH=$\frac{4}{5}$,
根据面积相等,可得$\frac{1}{2}$,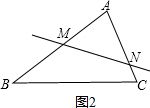
∴x=3(舍去,即为①)或x=5,
∴CF=5,CE=3,直线EF即为所求直线.
(b)直线与AB、AC分别交于M、N,如图2所示,
由(a)可得,AM=3,AN=5,直线MN即为所求直线.
(c)直线与AB、BC分别交于P、Q,如图4所示
过点A作AY⊥BC于点Y,过点P作PX⊥BC于点X
由面积法可得,AY=$\frac{24}{5}$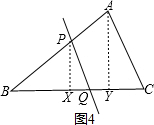 ,
,
设BP=x,则BQ=8-x,
由相似,可得PX=$\frac{24}{25}$,
根据面积相等,可得$\frac{1}{2}$,
∴x=$\frac{8+\sqrt{14}}{2}$(舍去)或x=$\frac{8-\sqrt{14}}{2}$.
而当BP=$\frac{8-\sqrt{14}}{2}$时,BQ=$\frac{8+\sqrt{14}}{2}$,舍去.
∴此种情况不存在,
综上所述,符合条件的直线共有三条.
点评 此题主要考查了相似三角形的综合应用以及相似三角形的判定与性质和等腰三角形的性质等知识,运用分类讨论的数学思想得出是解题关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:填空题
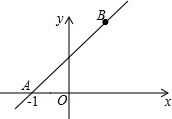 如图,在平面直角坐标系中,直线AB与x轴的夹角为45°,点A的坐标为(-1,0),点B在y轴右侧,设AB=2$\sqrt{2}$,那么点B的坐标为(1,2).
如图,在平面直角坐标系中,直线AB与x轴的夹角为45°,点A的坐标为(-1,0),点B在y轴右侧,设AB=2$\sqrt{2}$,那么点B的坐标为(1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y2<y3<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
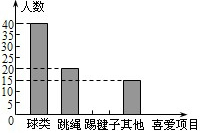 某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查,整理收集到的数据,绘制成如图所示的统计图.若该校共有1000名学生,估计喜欢“踢毽子”的学生有250人.
某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查,整理收集到的数据,绘制成如图所示的统计图.若该校共有1000名学生,估计喜欢“踢毽子”的学生有250人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
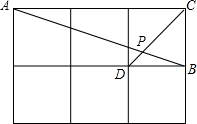 如图,在边长都为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,
如图,在边长都为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com