
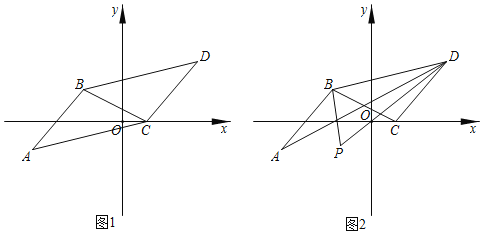
����Ŀ����ͼ����ͼ1����ƽ��ֱ������ϵ�У���֪��A����4����1����B����2��1�������߶�ABƽ�����߶�CD��ʹ��A�Ķ�Ӧ��C��x����������ϣ���D�ڵ�һ���ޣ�
��1������C�����꣨k��0�������D�����꣨�ú�k��ʽ�ӱ�ʾ����
��2������BD��BC����������BCD�����Ϊ5����k��ֵ��
��3����ͼ2���ֱ�����ABC�͡�ADC��ƽ���ߣ����ǽ��ڵ�P����д����A���͡�P�͡�BCD֮���һ��������ϵ����˵�����ɣ�
���𰸡���1��D��k+2��2������2��k��2����3����BPD��![]() ��BCD+
��BCD+![]() ��A�������������
��A�������������
��������
��1����ƽ�Ƶ����ʿɵó��𰸣�
��2������B��BE��x���ڵ�E������D��DF��x���ڵ�F�����ı���BEFD������ɵó��𰸣�
��3������P��PE��AB�ó���PBA����EPB����ƽ�Ƶ����ʵó�AB��CD����ƽ���ߵ����ʵó�PE��CD�����EPD����PDC���ó���BPD����PBA+��PDC���ɽ�ƽ���ߵ����ʵó���PBA��![]() ��ABC����PDC��
��ABC����PDC��![]() ��ADC�����ɵó����ۣ�
��ADC�����ɵó����ۣ�
�⣺��1���ߵ�A����4����1����B����2��1����C��k��0�������߶�ABƽ�����߶�CD��
���B����ƽ��һ����λ������ƽ�ƣ�k+4������λ����D��
��D��k+2��2����
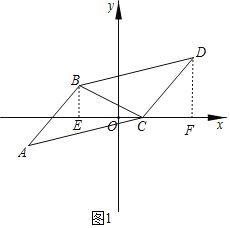
��2����ͼ1������B��BE��x���ڵ�E������D��DF��x���ڵ�F��
��A����4����1����B����2��1����C��k��0����D��k+2��2����
��BE��1��CE��k+2��DF��2��EF��k+4��CF��2��
��S�ı���BEFD��S��BEC+S��DCF+S��BCD��
��![]() ��
��![]() ��
��
��ã�k��2��
��3����BPD��![]() ��BCD+
��BCD+![]() ��A���������£�
��A���������£�
����P��PE��AB����ͼ2��ʾ��
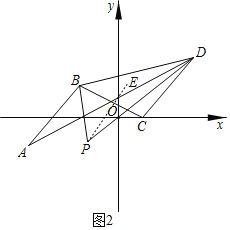
���PBA����EPB��
���߶�ABƽ�����߶�CD��
��AB��CD��
��PE��CD����ADC����A����ABC����BCD��
���EPD����PDC��
���BPD����PBA+��PDC��
��BPƽ�֡�ABC��DPƽ�֡�ADC��
���PBA��![]() ��ABC����PDC��
��ABC����PDC��![]() ��ADC��
��ADC��
���BPD��![]() ��ABC+
��ABC+![]() ��ADC��
��ADC��![]() ��BCD+
��BCD+![]() ��A��
��A��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1����:![]() ��
��
(2)�ⲻ��ʽ��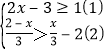
�����������,��ɱ���Ľ��:
�ⲻ��ʽ(1),��______________.
�ⲻ��ʽ(2),��_______________.
�Ѳ���ʽ(1)��(2)�Ľ⼯�������ϱ�ʾ����
![]()
��ԭ����ʽ��Ľ⼯Ϊ_________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
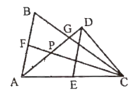
����Ŀ����ͼ����![]() �У�
�У�![]() ƽ��
ƽ��![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��ƽ����
��ƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() �����н��ۣ�
�����н��ۣ�
��![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ����_____________��
��������ȷ����_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AD��BC��AEƽ�֡�BAD��CD��AE�ཻ�ڵ�F����CFE=��E����˵��AB��DC���������˵�����̲���������
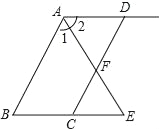
֤������AD��BC����֪��
���2=��E��___________________________��
��AEƽ�֡�BAD����֪��
���1=��2����_________________________��
���1=��E��___________________________��
�ߡ�CFE=��E����֪��
���1=��______��______________________��
��AB��CD��_________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���D��E�ֱ�ΪAB��AC���е㣬���ADE���ı���BCED�������Ϊ�� ��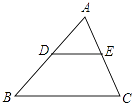
A.1��1
B.1��2
C.1��3
D.1��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ֱ��
ֱ��![]() ������Ϊ
������Ϊ![]() ��
��![]() ��ͼ���ã�����
��ͼ���ã�����![]() ��
��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ��ȡһ��
��ȡһ��![]() ������
������![]() ��
��![]() ��
��
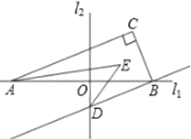
��1����![]() ��
��![]() ����
����![]() _______��
_______��
��2����![]() ��
��![]() ����
����![]() _______�������ú�
_______�������ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ�����������������Բ����ˮ���ڣ�����һ�����ٶ���ˮ����עˮ��![]() ʱע��ˮ�ۣ�ˮ����ˮ��ĸ߶�
ʱע��ˮ�ۣ�ˮ����ˮ��ĸ߶�![]() ��עˮʱ��
��עˮʱ��![]() ֮��ĺ���ͼ����ͼ2��ʾ.���������������ȡ�����־���____��ǡ�ý�ˮ��ע��.
֮��ĺ���ͼ����ͼ2��ʾ.���������������ȡ�����־���____��ǡ�ý�ˮ��ע��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ABC�ǵȱ������Σ�D��E�ֱ�Ϊ��BC��AC�ϵĵ㣬��BD��CE����D��BE��ƽ���ߣ���E��BC��ƽ���ߣ����ǽ��ڵ�F������AF��
��1����֤����ABE�ա�CAD��
��2�����жϡ�ADF����״����˵�����ɣ�
��3������D��E�ֱ���Ϊ��CB���ӳ��ߺ�AC���ӳ����ϵĵ㣬�����������䣨��ͼ�ڣ������ADF����״�Ƿ�ı䣬˵�����ɣ�
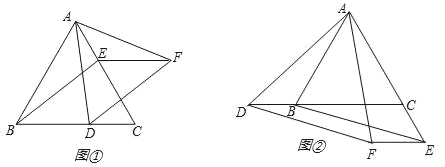
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ������һ����Ͷ�Ź������г�700�����������ó��У�����Ͷ������������ ���³�����Ҫ����ȴδ����������������ȡ��ij������ͬһʱ�εĵ������ݻ�����±���.
������һ����Ͷ�Ź������г�700�����������ó��У�����Ͷ������������ ���³�����Ҫ����ȴδ����������������ȡ��ij������ͬһʱ�εĵ������ݻ�����±���.
��ش���������:
ʱ�� | ��һ��7��00��8��00 | �ڶ���7��00��8��00 | ������7��00��8��00 | ������7��00��8��00 | ������7��00��8��00 |
��Ҫ�������г�ȴδ������������ˣ� | 1500 | 1200 | 1300 | 1300 | 1200 |
��1�������е�������ݣ�����������λ�������٣�
��2�����������������ƽ��ÿ����7:00-8:00 :��Ҫ���ù������г���������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com