
【题目】矩形ABCD中,AB=8,AD=6,P、Q是对角线BD上不重合的两点,点P关于直线AD,AB的对称点分别点E,F,点Q关于直线BC,CD的对称点分别是点G、H.若由点E,F,G,H构成的四边形恰好为菱形,则PQ的长为_____.
【答案】5.6
【解析】
根据轴对称求出AE=AF=AP,求出A、B、C、D都在菱形EFGH的边上,求出OA=AP=5,根据勾股定理求出ON,求出OP、OQ,即可得出答案.
矩形ABCD中,AB=8,AD=6,由勾股定理得:AC=BD=10,
如图,
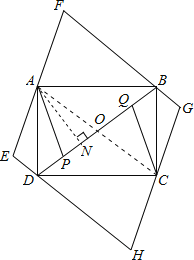
根据轴对称性质得:∠PAF+∠PAE=90°+90°=180°,
即A在菱形EFGH的边EF上,
同理B、C、D都在菱形EFGH的边上,
∵AP=AF=AE,即A为EF的中点,
同理C为GH的中点,
∵四边形EFGH是菱形,
∴AF=CG,AF∥CG,
∴四边形AFGC是平行四边形,
∴FG=AC=10,
∵AE=AF=AP,
∴AP=5,
∵AO=![]() AC=5,
AC=5,
∴AO=AP,
∴△APO是等腰三角形,
过A作AN⊥BD于N,
则N为OP的中点,
在Rt△DAB中,由三角形的面积公式得:AN×AB=×AD×AB,
∴AN=4.8,
由勾股定理得:ON=![]() =1.4,
=1.4,
则OP=2.8,
同理OQ=2.8,
所以PQ=2.8+2.8=5.6,
故答案为:5.6


科目:初中数学 来源: 题型:
【题目】现有四张完全相同的不透明卡片,其正面分别写有数字-2,-1,0,2,把这四张卡片背面朝上洗匀后放在桌面上.
(1)随机抽取一张卡片,求抽取的卡片上的数字为负数的概率;
(2)先随机抽取卡片,其上的数字作为点A的横坐标;然后放回并洗匀,再随机抽取一张卡片,其上的数字作为点A的纵坐标,试用画树状图或列表的方法求出点A在直线y=2x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈3.16)
≈3.16)

查看答案和解析>>
科目:初中数学 来源: 题型:
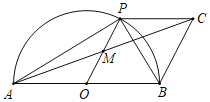
【题目】如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的动点,PC∥AB,点M是OP中点.
(1)求证:四边形OBCP是平行四边形;
(2)填空:
①当∠BOP= 时,四边形AOCP是菱形;
②连接BP,当∠ABP= 时,PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
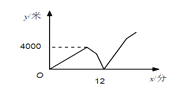
【题目】某公司快递员甲匀速骑车前往某小区送物件,出发几分钟后,快递员乙发现甲的手机落在公司,无法联系,于是乙匀速骑车去追赶甲.乙刚出发2分钟时,甲也发现自己手机落在公司,立刻按原路原速骑车回公司,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回公司,甲继续原路原速赶往某小区送物件,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(乙给甲手机的时间忽略不计).则乙回到公司时,甲距公司的路程是______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
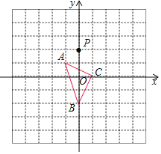
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,1),B(0,﹣2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2019的坐标为( )
A.(-2,0)B.![]() C.(2,-4)D.(-2,-2)
C.(2,-4)D.(-2,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
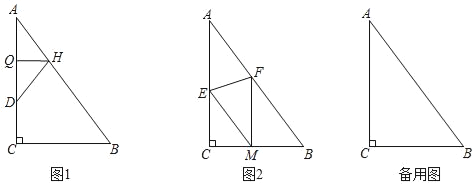
【题目】在△ABC中,∠ACB=90°,AB=25,BC=15.
(1)如图1,折叠△ABC使点A落在AC边上的点D处,折痕交AC、AB分别于Q、H,若S△ABC=9S△DHQ,则HQ= .
(2)如图2,折叠△ABC使点A落在BC边上的点M处,折痕交AC、AB分别于E、F.若FM∥AC,求证:四边形AEMF是菱形;
(3)在(1)(2)的条件下,线段CQ上是否存在点P,使得△CMP和△HQP相似?若存在,求出PQ的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com