
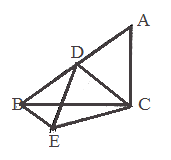
【题目】在△ABC中,∠BCA=90,AC=6,BC=8,D是AB的中点,将△ACD沿直线CD折叠得到△ECD,连接BE,则线段BE的长等于( )
A.5B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根据勾股定理及直角三角形的中线、翻折得CD=DE=BD=5,CE=AC=6,作DH⊥BE于H,EG⊥CD于G,证明△DHE≌△EGD,利用勾股定理求出![]() ,即可得到BE.
,即可得到BE.
∵∠BCA=90,AC=6,BC=8,
∴![]() ,
,
∵D是AB的中点,
∴AD=BD=CD=5,
由翻折得:DE=AD=5,∠EDC=∠ADC,CE=AC=6,
∴BD=DE,
作DH⊥BE于H,EG⊥CD于G,
∴∠DHE=∠EGD=90![]() ,∠EDH=
,∠EDH=![]() ∠BDE=
∠BDE=![]() (180
(180![]() -2∠EDC)=90
-2∠EDC)=90![]() -∠EDC,
-∠EDC,
∴∠DEB= 90![]() -∠EDH=90
-∠EDH=90![]() -(90
-(90![]() -∠EDC)=∠EDC,
-∠EDC)=∠EDC,
∵DE=DE,
∴△DHE≌△EGD,
∴DH=EG,EH=DG,
设DG=x,则CG=5-x,
∵![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴BE=2EH=![]() ,
,
故选:C.



科目:初中数学 来源: 题型:
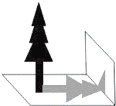
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
A.4.25mB.4.45mC.4.60mD.4.75m
查看答案和解析>>
科目:初中数学 来源: 题型:
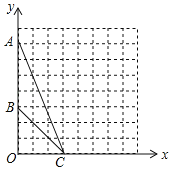
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
(1)在图中作出△ABC的外接圆(利用格图确定圆心);
(2)圆心坐标为 ;外接圆半径r为 ;
(2)若在x轴的正半轴上有一点D,且∠ADB=∠ACB,则点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣2x(a≠0)与x轴交于点A,B(点A在点B的左侧).
(1)当a=﹣1时,求A,B两点的坐标;
(2)过点P(3,0)作垂直于x轴的直线l,交抛物线于点C.
①当a=2时,求PB+PC的值;
②若点B在直线l左侧,且PB+PC≥14,结合函数的图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
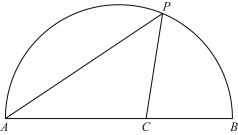
小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
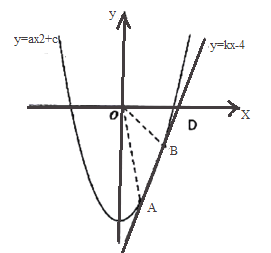
【题目】如图,设抛物线T:y=ax2+c(a> 0)与直线L:y=kx-4(k> 0)交A,B两点(点B在点A的右侧).
(1)如图,若点A(![]() ,-
,-![]() ),且a+c=-1.
),且a+c=-1.
①求抛物线T和直线L的解析式;
②求△AOB的面积.
(2)设点C是点B关于y轴的对称点,当点A,O,C三点共线时,求实数c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司根据市场需求销售A、B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等.
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划用不超过9.8万元购进A,B两种型号的净水器共50台,其中A型、B型净水器每台售价分别为2500元、2180元,设A型净水器为x台.
①求x的取值范围.
②若公司决定从销售A型净水器的利润中每台捐献a(100<a<150)元给贫困村饮水改造爱心工程,求售完这50台净水器后获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:t1,t2是方程t2+2t﹣24=0的两个实数根,且t1<t2,抛物线y=![]() x2+bx+c的图象经过点A(t1,0),B(0,t2).
x2+bx+c的图象经过点A(t1,0),B(0,t2).
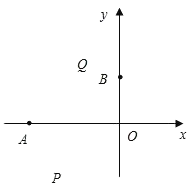
(1)求这个抛物线的解析式;
(2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求平行四边形OPAQ的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,当平行四边形OPAQ的面积为24时,是否存在这样的点P,使OPAQ为正方形?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园内有一个由两个全等的六边形(边长为![]() )围成的花坛,现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为( )
)围成的花坛,现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com