
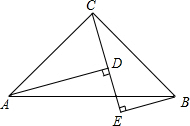
 如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于D,AD=5cm,DE=2cm,则BE的长为
如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于D,AD=5cm,DE=2cm,则BE的长为
|


科目:初中数学 来源: 题型:
 (2)已知乙车以60km/时的速度匀速行驶,设行驶过程中,两车的距离为s(km),请直接写出s关于x的表达式;
(2)已知乙车以60km/时的速度匀速行驶,设行驶过程中,两车的距离为s(km),请直接写出s关于x的表达式;查看答案和解析>>
科目:初中数学 来源: 题型:
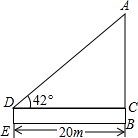 如图,升国旗时,某同学站在离国旗20m处行注目礼,当国旗升至顶端时,该同学视线的仰角为42°,已知双眼离地面1.60m,求旗杆AB的高度(精确到0.01m).
如图,升国旗时,某同学站在离国旗20m处行注目礼,当国旗升至顶端时,该同学视线的仰角为42°,已知双眼离地面1.60m,求旗杆AB的高度(精确到0.01m).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com