
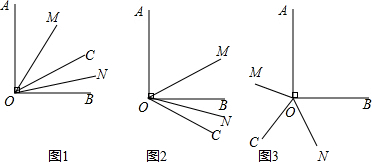
���� ��1�����ɽ�ƽ���ߵĶ��壬�������MOA�͡�NOA�Ķ�����Ȼ����������Ӽ��ɣ����ɽ�ƽ���ߵĶ��壬�������MOA�͡�NOA�Ķ�����Ȼ����������Ӽ��ɣ�
��2���ɽ�ƽ���ߵĶ��壬�������MOA�͡�NOA�Ķ�����Ȼ��������������ɣ�
��3���ɽ�ƽ���ߵĶ��壬�������MOA�͡�NOA�Ķ�����Ȼ����������Ӽ��ɣ�
��� �⣺��1���١ߡ�AOB=90�㣬��BOC=30�㣬
���AOC=60�㣬
��OM��ON�ֱ�ƽ�֡�AOC����BOC��
���COM=$\frac{1}{2}��$AOC��$��CON=\frac{1}{2}��$BOC��
���MON=��COM+��CON=$\frac{1}{2}$��AOB=45�㣬
�ʴ�Ϊ��45�㣬
�ڡߡ�AOB=90�㣬��BOC=n�㣬
���AOC=��90-n���㣬
��OM��ON�ֱ�ƽ�֡�AOC����BOC��
���COM=$\frac{1}{2}��$AOC=$\frac{1}{2}$��90-n���㣬$��CON=\frac{1}{2}��$BOC=$\frac{1}{2}$n�㣬
���MON=��COM+��CON=$\frac{1}{2}$��AOB=45�㣬
�ʴ�Ϊ��45�㣻
��2���ߡ�AOB=90�㣬���BOC=����
���AOC=90��+����
��OM��ON�ֱ�ƽ�֡�AOC����BOC��
���COM=$\frac{1}{2}��$AOC��$��CON=\frac{1}{2}��$BOC��
���MON=��COM-��CON=$\frac{1}{2}$��AOB=45�㣬
��3����OM��ON�ֱ�ƽ�֡�AOC����BOC��
���COM=$\frac{1}{2}��$AOC��$��CON=\frac{1}{2}��$BOC��
���MON=��COM+��CON=$\frac{1}{2}$����AOC+��BOC��=$\frac{1}{2}$��360��-90�㣩=135�㣮
���� ���⿼���˽�ƽ���߶��壬�ǵ��йؼ����Ӧ�ã������Ĺؼ��������COM�͡�CON�Ĵ�С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪a��b��cΪ���������������������ϵ�λ����ͼ��ʾ��
��֪a��b��cΪ���������������������ϵ�λ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
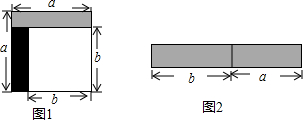
 ��ͼ��һ���߳�Ϊ6��������ľ�䣬��Q���ϵ�������ϣ�AQ=2��һֻ���ϴ�P�������ľ��������е���Q�����������е����·�̣�
��ͼ��һ���߳�Ϊ6��������ľ�䣬��Q���ϵ�������ϣ�AQ=2��һֻ���ϴ�P�������ľ��������е���Q�����������е����·�̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����A��B��C��D��E��FΪ��O�����ȷֵ㣬����P��Բ��O��������OE��EFFO��·���������˶������˶���ʱ��Ϊt����BPD�Ķ���Ϊy��������ͼ���б�ʾy��t֮�亯����ϵ��ǡ�����ǣ�������
��ͼ����A��B��C��D��E��FΪ��O�����ȷֵ㣬����P��Բ��O��������OE��EFFO��·���������˶������˶���ʱ��Ϊt����BPD�Ķ���Ϊy��������ͼ���б�ʾy��t֮�亯����ϵ��ǡ�����ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 15�� | B�� | 85�� | C�� | 120�� | D�� | 135�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com