
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为项点作等腰直角三角形
为项点作等腰直角三角形![]() ,使
,使![]() ,连接
,连接![]() ,射线
,射线![]() 交
交![]() 于点
于点![]() .
.
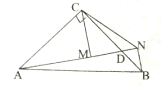
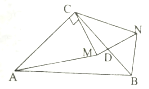
图1 图2
(1)如图1,若点![]() 、
、![]() 、
、![]() 在一条直线上,
在一条直线上,
①求证:![]() ;
;
②若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,若![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一周,在旋转过程中射线
顺时针旋转一周,在旋转过程中射线![]() 交于
交于![]() 点
点![]() ,当三角形
,当三角形![]() 是直角三角形时,请你直接写出
是直角三角形时,请你直接写出![]() 的长.
的长.
【答案】(1)①见解析,②![]() ;(2)
;(2)![]() 或2
或2
【解析】
(1)①如图,过点C作CF⊥CN,交AN于点F,由等腰直角三角形的性质,可求∠CNM=45°,CM=MN,即可证∠FCN=∠ACB,∠CFN=∠CNF=45°,根据“SAS”可证△ACF≌△BCN,可得AF=BN,根据等腰直角三角形的性质可得MF=MN=CM,即可证BN+CM=AM;
②由题意可求出CM=MN=![]() ,由全等三角形的性质可得∠CAF=∠CBN,即可证∠MCD=∠CBN,则CM∥BN,可得△MCD∽△NBD,根据相似三角形的性质和勾股定理可求BD的长;
,由全等三角形的性质可得∠CAF=∠CBN,即可证∠MCD=∠CBN,则CM∥BN,可得△MCD∽△NBD,根据相似三角形的性质和勾股定理可求BD的长;
(2)分∠BDH=90°,∠DHB=90°两种情况讨论,根据等腰直角三角形的性质可求CD的长.
证明:(1)①如图,过点C作CF⊥CN,交AN于点F,
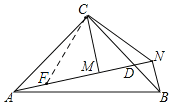
∵△CMN是等腰直角三角形,
∴∠CNM=45°,CM=MN,
∵CF⊥CN,∠ACB=90°,
∴∠FCN=∠ACB,∠CFN=∠CNF=45°,
∴∠ACF=∠BCN,CF=CN,且AC=BC,
∴△ACF≌△BCN(SAS),
∴AF=BN,
∵CF=CN,CM⊥MN,
∴MF=MN=CM,
∴AM=AF+FM=BN+CM;
②∵AM=4,BN=![]() ,BN+CM=AM,
,BN+CM=AM,
∴CM=MN=![]() ,
,
∵△ACF≌△BCN,
∴∠CAF=∠CBN,
∵∠CAF+∠ACF=∠CFN=45°,∠BCN+∠MCD=∠MCN=45°,
∴∠CAF=∠MCD,且∠CAF=∠CBN,
∴∠MCD=∠CBN,
∴CM∥BN,
∴△MCD∽△NBD,∠CMD=∠BND=90°,
∴![]()
∴MD=![]() ND,
ND,
∵MD+ND=MN=![]() ,
,
∴ND=![]() ,
,
在Rt△DNB中,BD=![]() ,
,
(2)若∠BDH=90°,如图,此时点M与点D重合,
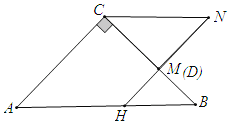
∵△CMN是等腰直角三角形,CN=2,
∴CM=MN=![]() ,
,
∴CD=![]() ,
,
若∠BHD=90°,如图,
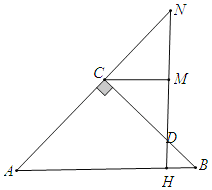
∵∠BHD=90°,∠B=45°,
∴∠BDH=45°,
∴∠CDN=45°=∠N,
∴CD=CN=2.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
查看答案和解析>>
科目:初中数学 来源: 题型:
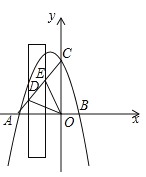
【题目】如图,抛物线![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
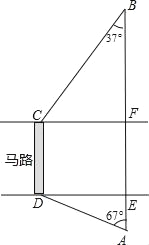
【题目】如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市,CD与AB所在直线互相平行,且都与马路的两边垂直.马路宽20米,A,B相距62米,∠A=67°,∠B=37°.求CD与AB之间的距离.(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,sn37°≈
,sn37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为半圆的直径,点
为半圆的直径,点![]() 为圆心,
为圆心,![]() 为半圆的切线,过半圆上的点
为半圆的切线,过半圆上的点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)连接![]() ,若
,若![]() ,求证:
,求证:![]() 是半圆的切线;
是半圆的切线;
(2)如图2,当线段![]() 与半圆交于点
与半圆交于点![]() 时,连接
时,连接![]() ,
,![]() ,判断
,判断![]() 和
和![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() .有下列结论:①
.有下列结论:①![]() ; ②当
; ②当![]() 时,随x的增大而增大;③当
时,随x的增大而增大;③当![]() 时,
时,![]() ;④当
;④当![]() 时,若二次函数的最小值为
时,若二次函数的最小值为![]() ,则m的取值范围是
,则m的取值范围是![]() 。其中正确结论的个数是( )
。其中正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com