
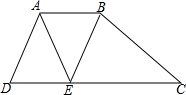
 如图,在四边形ABCD中,AB∥CD,AB=4,CD=11,点E在边CD上,AD∥BE,若AD=AB,且cos∠BEC=$\frac{1}{2}$,则四边形ABCE的面积为( )
如图,在四边形ABCD中,AB∥CD,AB=4,CD=11,点E在边CD上,AD∥BE,若AD=AB,且cos∠BEC=$\frac{1}{2}$,则四边形ABCE的面积为( )| A. | $\sqrt{3}$ | B. | 11$\sqrt{3}$ | C. | 15$\sqrt{3}$ | D. | 22$\sqrt{3}$ |
分析 过B作BF⊥DC于F,根据菱形的判定得出四边形ADEB是菱形,根据菱形的性质求出BE=4,根据cos∠BEC=$\frac{1}{2}$求出EF和BF,根据梯形的面积公式求出即可.
解答 解:如图,过B作BF⊥DC于F,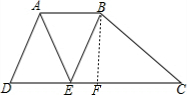
∵AD∥BE,AB∥DE,AD=AB=4,
∴四边形ADEB是菱形,
∴BE=4,
∵cos∠BEC=$\frac{1}{2}$,
∴EF=$\frac{1}{2}$BE=2,
由勾股定理得:BF=$\sqrt{B{E}^{2}-E{F}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
则四边形ABCE的面积为:$\frac{1}{2}$×(AB+CD)×BF=$\frac{1}{2}×$(4+11)×2$\sqrt{3}$=15$\sqrt{3}$,
故选C.
点评 本题考查了勾股定理,菱形的性质和判定的应用,能求出梯形的高是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
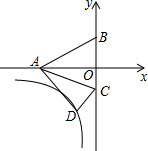 如图,在平面直角坐标系中有一个Rt△ABO,点A的坐标为(-2,0),点B的坐标为(0,1),将△ABO绕点A按顺时针方向旋转45°,点O的对应点D恰好落在双曲线y=$\frac{k}{x}$(x<0)上,在此双曲线上存在一点E,若点E到x轴的距离为2,则点E的坐标为( )
如图,在平面直角坐标系中有一个Rt△ABO,点A的坐标为(-2,0),点B的坐标为(0,1),将△ABO绕点A按顺时针方向旋转45°,点O的对应点D恰好落在双曲线y=$\frac{k}{x}$(x<0)上,在此双曲线上存在一点E,若点E到x轴的距离为2,则点E的坐标为( )| A. | (-2,1-$\sqrt{2}$) | B. | (-2,$\sqrt{2}-1$) | C. | (1-$\sqrt{2}$,-2) | D. | ($\sqrt{2}-1,-2$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某企业为一商场提供家电配件,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
某企业为一商场提供家电配件,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com