
 如图,在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=DC.试判断AC与CE的大小关系?并说明理由.
如图,在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=DC.试判断AC与CE的大小关系?并说明理由.
|


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
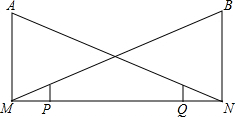 如图,王军同学上完晚自习放学步行回家,由路灯A走向路灯B,当他走到点P时,发现身后的影子顶部刚好接触到路灯A的底部M,当他向前再步行12m到达点Q时,发现身前他影子的顶部刚好接触到路灯B的底部N.已知王军的身高是1.6m,路灯A的高度AM是9.6m,且MP=NQ=x m.
如图,王军同学上完晚自习放学步行回家,由路灯A走向路灯B,当他走到点P时,发现身后的影子顶部刚好接触到路灯A的底部M,当他向前再步行12m到达点Q时,发现身前他影子的顶部刚好接触到路灯B的底部N.已知王军的身高是1.6m,路灯A的高度AM是9.6m,且MP=NQ=x m.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)先观察下列等式,再完成题后问题:
(1)先观察下列等式,再完成题后问题:| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2010×2011 |
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2009)(b+2009) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com