练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．下列图形中，既是中心对称图形又是轴对称图形的有（　　）个．
    ①线段；②等边三角形；③矩形；④菱形；⑤平行四边形．
    A．3个B．4个C．5个D．2个

    分析 根据轴对称图形与中心对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．
    如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．

    解答 解：①线段既是轴对称图形，又是中心对称图形．符合题意；
    ②等边三角形是轴对称图形，不是中心对称图形．不符合题意；
    ③矩形是轴对称图形，又是中心对称图形．符合题意；
    ④菱形既是轴对称图形，又是中心对称图形．符合题意．
    ⑤平行四边形不是轴对称图形，是中心对称图形．不符合题意；
    既是轴对称图形又是中心对称图形的有3个．
    故选：A．

    点评 本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形沿对称轴折叠后可重合；中心对称图形关键是要寻找对称中心，图形旋转180°后与原图重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    20．从边长为（a+1）cm的正方形纸片中剪去一个边长为（a-1）cm的正方形（a＞1），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则该矩形的面积是4a．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．关于x的方程$\frac{n}{x-1}+\frac{m}{x-2}=0$可能产生的增根是（　　）
    A．x=1B．x=2C．x=1或x=2D．x=一1或=2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．小明根据某个一次函数关系式填写了如下的表格：其中有一格不慎被墨汁遮住了，想想看，该空格里原来填的数是（　　）
    x2-101
    y310
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

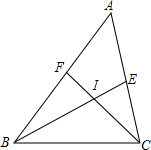    5．如图，△ABC中，∠ABC和∠ACB的角平分线相交于点I，爱动脑筋的小明同学在写作业时，发现了如下规律：
    （1）若∠A=50°，则∠BIC=115°=90°+$\frac{50°}{2}$；
    （2）若∠A=90°，则∠BIC=135°=90°+$\frac{90°}{2}$；
    （3）若∠A=130°，则∠BIC=155°=90°+$\frac{130°}{2}$；
    （4）根据上述规律，或∠A=150°，则∠BIC=165°．
    （5）请你用数学表达式归纳出∠BIC与∠A的关系：∠BIC=90°+$\frac{1}{2}$∠A．
    （6）请证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图1，已知线段AB、CD相交于点O，连接AC、BD，我们把形如图1的图形称之为“8字形”．如图2，∠CAB和∠BDC的平分线AP和DP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：
    （1）仔细观察，在图2中有3个以线段AC为边的“8字形”；
    （2）在图2中，若∠B=96°，∠C=100°，求∠P的度数．
    （3）在图2中，若设∠C=α，∠B=β，∠CAP=$\frac{1}{3}$∠CAB，∠CDP=$\frac{1}{3}$∠CDB，试问∠P与∠C、∠B之间存在着怎样的数量关系（用α、β表示∠P），并说明理由；
    （4）如图3，则∠A+∠B+∠C+∠D+∠E+∠F的度数为360°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．已知x1，x2是关于x的方程（x-2）（x-3）=（n-2）（n-3）的两个实数根．则：
    （1）两实数根x1，x2的和是5；
    （2）若x1，x2恰是一个直角三角形的两直角边的边长，那么这个直角三角形面积的最大值是$\frac{25}{8}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

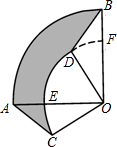    19．如图，把两个扇形OAB与扇形OCD的圆心重合叠放在一起，且∠AOB=∠COD，连接AC．
    （1）求证：△AOC≌△BOD；
    （2）若OA=3cm，OC=2cm，弧AB的长为$\frac{3π}{2}$，弧CD的长为π，求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．规定[x]的值为不大于x的最大实数．如[2.1]=2，[-3.8]=-4，则[$\sqrt{3}$-1]的值为0．

    查看答案和解析>>

    同步练习册答案