
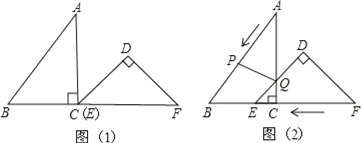
【题目】把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).
(1)用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;
(2)连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;
(3)当t为何值时,△APQ是等腰三角形.
【答案】(1)AP=2t,AQ=8﹣t,t的取值范围是:0≤t≤5;(2)![]() cm2;(3)
cm2;(3)![]() 或
或![]() 或
或![]() 时,△APQ是等腰三角形.
时,△APQ是等腰三角形.
【解析】试题分析:(1)根据题意以及直角三角形性质表达出CQ、AQ,从而得出结论,
(2)作PG⊥x轴,将四边形的面积表示为S△ABC﹣S△BPE﹣S△QCE即可求解,
(3)根据题意以及三角形相似对边比例性质即可得出结论.
(1)解:AP=2t
∵∠EDF=90°,∠DEF=45°,
∴∠CQE=45°=∠DEF,
∴CQ=CE=t,
∴AQ=8﹣t,
t的取值范围是:0≤t≤5;
(2)过点P作PG⊥x轴于G,可求得AB=10,SinB=![]() ,PB=10﹣2t,EB=6﹣t,
,PB=10﹣2t,EB=6﹣t,
∴PG=PBsinB=![]() (10﹣2t)
(10﹣2t)
∴y=S△ABC﹣S△PBE﹣S△QCE=![]()
= ![]()
=![]()
∴当![]() (在0≤t≤5内),y有最大值,y最大值=
(在0≤t≤5内),y有最大值,y最大值=![]() (cm2)
(cm2)
(3)若AP=AQ,则有2t=8﹣t解得: ![]() (s)
(s)
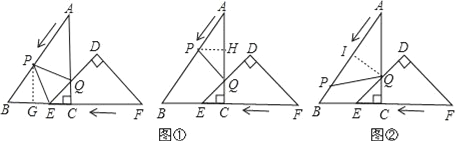
若AP=PQ,如图①:过点P作PH⊥AC,则AH=QH=![]() ,PH∥BC
,PH∥BC
∴△APH∽△ABC,
∴![]() ,
,
即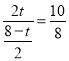 ,
,
解得: ![]() (s)
(s)
若AQ=PQ,如图②:过点Q作QI⊥AB,则AI=PI=![]() AP=t
AP=t
∵∠AIQ=∠ACB=90°∠A=∠A,
∴△AQI∽△ABC
∴![]()
即![]() ,
,
解得: ![]() (s)
(s)
综上所述,当![]() 或
或![]() 或
或![]() 时,△APQ是等腰三角形.
时,△APQ是等腰三角形.


科目:初中数学 来源: 题型:
【题目】假如你想知道你们班同学的身高情况,你必须进行调查,然后对你的调查结果加以总结,那么:
(1)你调查的问题是 ;
(2)你调查的对象是;
(3)你感兴趣的是调查对象的 ;
(4)你的调查方式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当x分别取﹣ ![]() 、﹣
、﹣ ![]() 、﹣
、﹣ ![]() 、…、﹣
、…、﹣ ![]() 、﹣2、﹣1、0、1、2、…、2015、2016、2017时,计算分式
、﹣2、﹣1、0、1、2、…、2015、2016、2017时,计算分式 ![]() 的值,再将所得结果相加,其和等于 .
的值,再将所得结果相加,其和等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a,b,c是同一平面内的三条不同直线,下列命题是假命题的是( )
A. 若a∥b,b∥c,则a∥cB. 若a⊥b,b⊥c,则a⊥c
C. 若a∥b, b⊥c,则a⊥cD. 若a⊥b,b⊥c,则a∥c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下各组线段为边,能组成三角形的是( )
A. 8cm,6cm,4cm B. 2cm,4cm,6cm
C. 14cm,6cm,7cm D. 2cm,3cm,6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
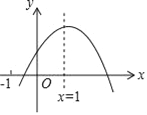
【题目】已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a﹣b+c<0;③2a+b﹣c<0;④4a+2b+c>0,⑤若点(﹣![]() ,y1)和(
,y1)和(![]() ,y2)在该图象上,则y1>y2.其中正确的结论是_____(填入正确结论的序号)
,y2)在该图象上,则y1>y2.其中正确的结论是_____(填入正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式4x2﹣16y2的结果是( )
A.(2x﹣4y)2
B.(2x﹣4y)(2x+4y)
C.4(x2﹣4y2)
D.4(x﹣2y)(x+2y)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com