
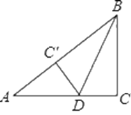
【题目】如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是____.
【答案】![]()
【解析】
先根据勾股定理求出AB的长,再由图形翻折变换的性质得出BC′的长及CD=C′D,设C′D=x,在Rt△ADC′中利用勾股定理即可求出C′D的长,利用三角形的面积公式即可求出△ADC'的面积.
∵在Rt△ABC中,∠C=90°,BC=3,AC=4,
∴AB=![]()
∵△BDC′是△BDC翻折变换而成,BC=3,AC=4,
∴CD=C′D,BC=BC′=3,∠BC′D=90°,
∴∠AC′D=90°,
∴△ADC′是直角三角形,
设C′D=x,则AD=4-x,
在Rt△ADC′中,AD2=AC′2+C′D2,即(4-x)2=(5-3)2+x2,
解得x=![]()
AC′=AB-BC′=5-3=2,
∴S△ADC′=![]() C′D×AC′=
C′D×AC′=![]() ×
×![]() ×2=
×2=![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线![]() 为抛物线
为抛物线![]() 、b、c为常数,
、b、c为常数,![]() 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.

已知抛物线![]() 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,与x轴负半轴交于点C.
,与x轴负半轴交于点C.
![]() 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
![]() 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将![]() 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若![]() 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标;
![]() 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() 轴于点
轴于点![]() .将抛物线
.将抛物线![]() 平移后得到顶点为
平移后得到顶点为![]() 且对称轴为直
且对称轴为直![]() 的抛物线
的抛物线![]() .
.
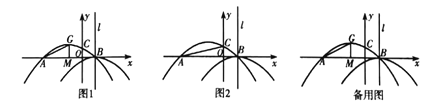
(1)求抛物线![]() 的解析式;
的解析式;
(2)如图2,在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,请求出所有点
是等腰三角形?若存在,请求出所有点![]() 的坐标:若不存在,请说明理由;
的坐标:若不存在,请说明理由;
(3)点![]() 为抛物线
为抛物线![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴的平行线交抛物线
轴的平行线交抛物线![]() 于点
于点![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,若以
,若以![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,求直线
全等,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
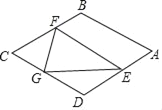
【题目】如图,在菱形ABCD中,AB=![]() ,∠B=120°,点E是AD边上的一个动点(不与A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.若△EFG是等腰三角形,则DE的长为_____.
,∠B=120°,点E是AD边上的一个动点(不与A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.若△EFG是等腰三角形,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
![]() 甲、乙两组工作一天,商店各应付多少钱?
甲、乙两组工作一天,商店各应付多少钱?
![]() 已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
![]() 装修完毕第二天即可正常营业,且每天仍可盈利200元
装修完毕第二天即可正常营业,且每天仍可盈利200元![]() 即装修前后每天盈利不变
即装修前后每天盈利不变![]() ,你认为商店应如何安排施工更有利?说说你的理由
,你认为商店应如何安排施工更有利?说说你的理由![]() 可用
可用![]() 问的条件及结论
问的条件及结论![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是数学史上非常重要的一个定理.早在![]() 多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以
多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以![]() 的三边为边长,向外作正方形
的三边为边长,向外作正方形![]() 、
、![]() 、
、![]() .
.
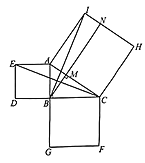
(1)连接![]() 、
、![]() ,求证:
,求证:![]()
(2)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
①试说明四边形![]() 与正方形
与正方形![]() 的面积相等;
的面积相等;
②请直接写出图中与正方形![]() 的面积相等的四边形.
的面积相等的四边形.
(3)由第(2)题可得:正方形![]() 的面积
的面积![]() 正方形
正方形![]() 的面积
的面积![]() _______________的面积,即在
_______________的面积,即在![]() 中,
中,![]() __________________.
__________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com