
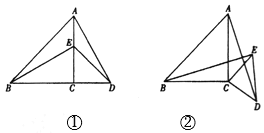
【题目】如图①,在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上任意一点(点
上任意一点(点![]() 与点
与点![]() ,
,![]() 不重合),以
不重合),以![]() 为一直角边作
为一直角边作![]() ,
,![]() ,连接
,连接![]() ,
,![]() .若
.若![]() 和
和![]() 是等腰直角三角形.
是等腰直角三角形.
(1)猜想线段![]() ,
,![]() 之间的数量关系及所在直线的位置关系,直接写出结论;
之间的数量关系及所在直线的位置关系,直接写出结论;
(2)现将图①中的![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,得到图②,请判断(1)中的结论是否仍然成立,若成立,请证明;若不成立,请说明理由.
,得到图②,请判断(1)中的结论是否仍然成立,若成立,请证明;若不成立,请说明理由.
【答案】(1)BE=AD,BE⊥AD ;(2)BE=AD,BE⊥AD仍然成立,理由见解析
【解析】
(1)由CA=CB,CE=CD,∠ACB=90°易证△BCE≌△ACD,所以BE=AD,∠BEC=∠ADC,又因为∠EBC+∠BEC=90°,所以∠EBC+∠ADC=90°,即BE⊥AD;
(2)成立.设BE与AC的交点为点F,BE与AD的交点为点G,易证△ACD≌△BCE.得到AD=BE,∠CAD=∠CBE.再根据等量代换得到∠AFG+∠CAD=90°.即BE⊥AD.
(1)BE=AD,BE⊥AD;
在△BCE和△ACD中,
∵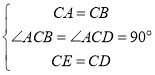 ,
,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠BEC=∠ADC,
∵∠EBC+∠BEC=90°,
∴∠EBC+∠ADC=90°,
∴BE⊥AD.
故答案为:BE=AD,BE⊥AD.
(2)BE=AD,BE⊥AD仍然成立
设BE与AC的交点为F,BE与AD的交点为G,如图
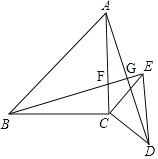
∴![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
∵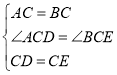
∴![]() .
.
∴![]()
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴BE⊥AD


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论:①a﹣b+c<0;②2a+b+c>0;③x(αx+b)≤a+b;④a>﹣1.其中正确的有( )
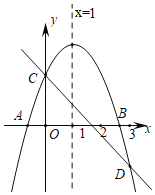
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3张正面分别写有数字![]() ,0,1的卡片,它们的背面完全相同,现将这3张卡片背面朝上洗匀,小明先从中任意抽出一张卡片记下数字为x;小亮再从剩下的卡片中任意取出一张记下数字为y,记作
,0,1的卡片,它们的背面完全相同,现将这3张卡片背面朝上洗匀,小明先从中任意抽出一张卡片记下数字为x;小亮再从剩下的卡片中任意取出一张记下数字为y,记作![]() .
.
![]() 用列表或画树状图的方法列出所有可能的点P的坐标;
用列表或画树状图的方法列出所有可能的点P的坐标;
![]() 若规定:点
若规定:点![]() 在第二象限小明获胜;点
在第二象限小明获胜;点![]() 在第四象限小亮获胜,游戏规则公平吗?
在第四象限小亮获胜,游戏规则公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市有![]() ,
,![]() 两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,且无剩油);当日促销活动:购买
两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,且无剩油);当日促销活动:购买![]() 型瓶3个或以上,一次性返还现金5元,设购买
型瓶3个或以上,一次性返还现金5元,设购买![]() 型瓶
型瓶![]() (个),所需总费用为
(个),所需总费用为![]() (元),则下列说法不一定成立的是( )
(元),则下列说法不一定成立的是( )
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
A.购买![]() 型瓶的个数是
型瓶的个数是![]() 为正整数时的值B.购买
为正整数时的值B.购买![]() 型瓶最多为6个
型瓶最多为6个
C.![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() D.小张买瓶子的最少费用是28元
D.小张买瓶子的最少费用是28元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 边以每秒1个单位长度的速度运动到点
边以每秒1个单位长度的速度运动到点![]() 时停止,连接
时停止,连接![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() ,
,![]() ,设运动时间为
,设运动时间为![]() (秒).
(秒).

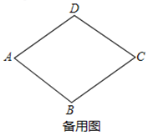
(1)菱形![]() 对角线
对角线![]() 的长为 ;
的长为 ;
(2)当点![]() 恰在
恰在![]() 上时,求t的值;
上时,求t的值;
(3)当![]() 时,求
时,求![]() 的周长;
的周长;
(4)直接写出在整个运动过程中,点![]() 运动的路径长.
运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
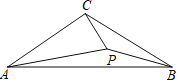
【题目】如图,若![]() 内一点
内一点![]() 满足
满足![]() ,则称点
,则称点![]() 为
为![]() 的布罗卡尔点,三角形的布罗卡尔点是法国数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知
的布罗卡尔点,三角形的布罗卡尔点是法国数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的布罗卡尔点,若
的布罗卡尔点,若![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 和直线
和直线![]() .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x= 1 .
其中正确的有

A.1个 B.2个 C. 3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
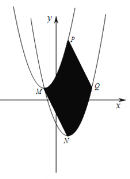
【题目】如图,抛物线![]() 和抛物线
和抛物线![]() 的顶点分别为点M和点N,线段MN经过平移得到线段PQ,若点Q的横坐标是3,则点P的坐标是__________,MN平移到PQ扫过的阴影部分的面积是__________.
的顶点分别为点M和点N,线段MN经过平移得到线段PQ,若点Q的横坐标是3,则点P的坐标是__________,MN平移到PQ扫过的阴影部分的面积是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com