Question

16．已知直线AB分别交x、y轴于A（a，0）、B两点，C（c，4）为直线AB上且在第二象限内一点，若$\sqrt{{c^2}-16}+{a^2}+16=8a$
（1）如图1，求A、C点的坐标；
（2）如图2，直线OM经过O点，过C作CM⊥OM于M，CN⊥y轴于点N，连MN，求式子$\frac{MO+MC}{MN}$的值；
（3）如图3，过C作CN⊥y轴于点N，G为第一象限内一点，且∠NGO=45°，试探究GC、GN、GO之间的数量关系并说明理由．

Answer 1

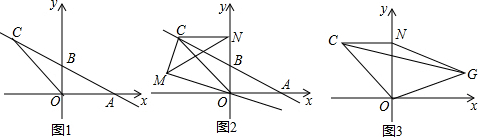
分析 （1）根据非负数的性质即可求出a、c的值．
（2）如图2中，作NQ⊥OM于Q，NP⊥MC于P，先证明△NCP≌△NOQ得PC=OQ，PN=QN，再证明四边形MQNP是正方形，由MN=$\sqrt{2}$MQ，MO+MC=2MQ即可解决问题．
（3）结论：GC²=OG²+2GN²，如图3中，作OP⊥NG于P，CQ⊥GN于Q，先证明△NCQ≌△ONP，设NQ=OP=PG=a，CQ=NP=b，用a、b的代数式表示GC²，GN²，OG²即可证明．

解答 解：（1）∵$\sqrt{{c}^{2}-16}+{a}^{2}+16=8a$，
∴$\sqrt{{c}^{2}-16}$+（a-4）²=0，
∵$\sqrt{{c}^{2}-16}$≥0，（a-4）²≥0，
∴c=±4，a=4，
∵点C在第二象限，
∴c=-4，
∴点A（4，0），点C（-4，4）．
（2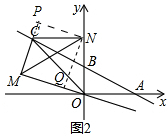）如图2中，作NQ⊥OM于Q，NP⊥MC于P，
∵∠PMO=∠MPN=∠NQM=90°，
∴四边形MQNP是矩形，
∴∠PNQ=∠CNO=90°，
∴∠PNC=∠ONQ，
在△NCP和△NOQ中，
$\left\{\begin{array}{l}{∠P=∠NQO=90°}\\{∠PNC=∠ONQ}\\{CN=NO}\end{array}\right.$，
∴△NCP≌△NOQ，
∴NP=NQ，PC=OQ，
∴四边形MQNP是正方形，NM=$\sqrt{2}$MQ，
∴$\frac{MO+MC}{MN}$=$\frac{MQ+OQ+PM-PC}{MN}$=$\frac{2MQ}{\sqrt{2}MQ}$=$\sqrt{2}$．
（3）结论：GC²=OG²+2GN²
理由：如图3中，作OP⊥NG于P，CQ⊥GN于Q．
∵∠CNQ+∠ONP=90°，∠ONP+∠NOP=90°，
∴∠CNQ=∠NOP，
在△NCQ和△ONP中，
$\left\{\begin{array}{l}{∠CNQ=∠NOP}\\{∠Q=∠OPN}\\{CN=ON}\end{array}\right.$，
∴△NCQ≌△ONP，
∴NQ=OP=PG，CQ=NP，设NQ=OP=PG=a，CQ=NP=b，∵GC²=CQ²+QG²=b²+（2a+b）²=4a²+4ab+2b²，GN²=（a+b）²=a²+2ab+b²，GO²=OP²+PG²=a²+a²=2a²，
∴GC²=OG²+2GN²．

点评 本题考查全等三角形的判定和性质、坐标与图形的性质、正方形的判定和性质，解题的关键是添加辅助线构造全等三角形，最后一个问题体现了数形结合的思想，属于中考压轴题．